 detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2% detected=47.7% / unexpected=0.0%
detected=47.7% / unexpected=0.0% detected=84.8% / unexpected=0.9%
detected=84.8% / unexpected=0.9% detected=58.3% / unexpected=0.2%
detected=58.3% / unexpected=0.2%
 detected=94.7% / unexpected=0.1%
detected=94.7% / unexpected=0.1% detected=89.4% / unexpected=0.0%
detected=89.4% / unexpected=0.0% detected=73.5% / unexpected=1.2%
detected=73.5% / unexpected=1.2% detected=41.7% / unexpected=0.0%
detected=41.7% / unexpected=0.0%
 detected=100.0% / unexpected=0.8%
detected=100.0% / unexpected=0.8% detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%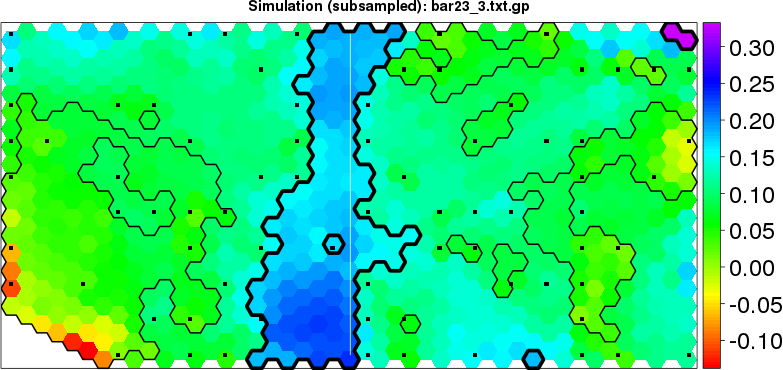 detected=100.0% / unexpected=0.4%
detected=100.0% / unexpected=0.4%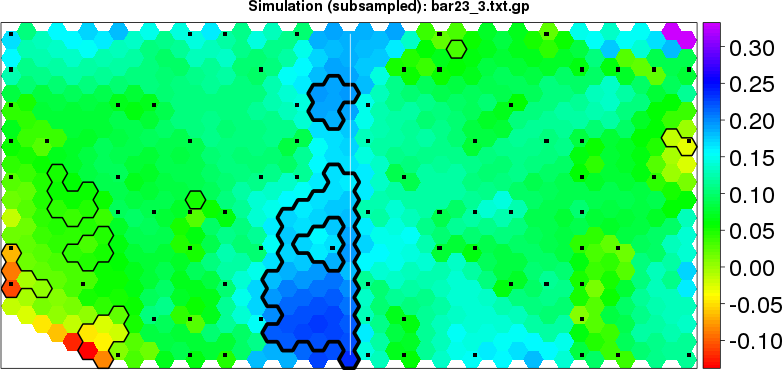 detected=63.6% / unexpected=0.0%
detected=63.6% / unexpected=0.0%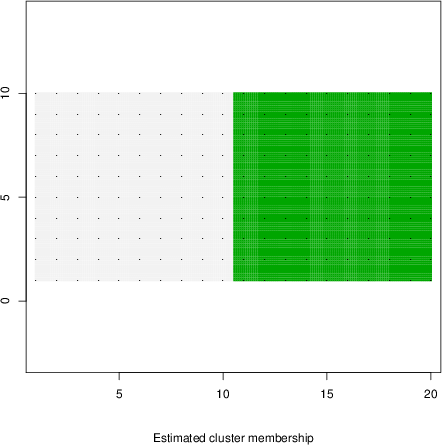
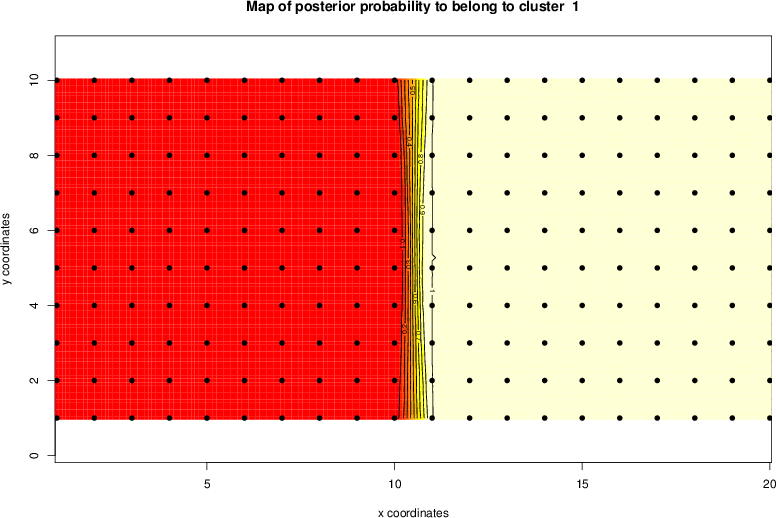
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=79.5% / unexpected=0.5%
detected=79.5% / unexpected=0.5% detected=42.4% / unexpected=0.2%
detected=42.4% / unexpected=0.2%
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2%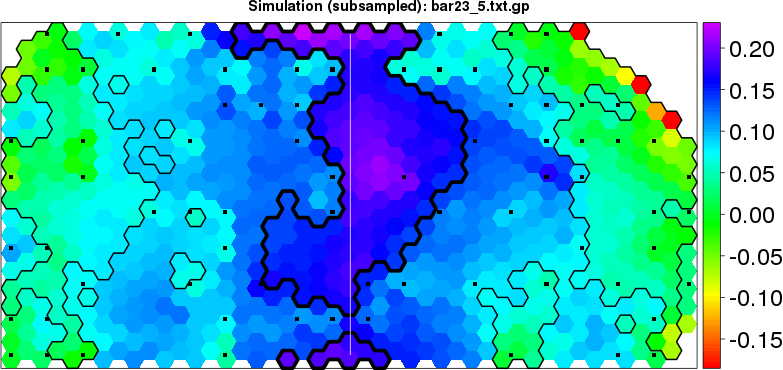 detected=94.7% / unexpected=0.1%
detected=94.7% / unexpected=0.1%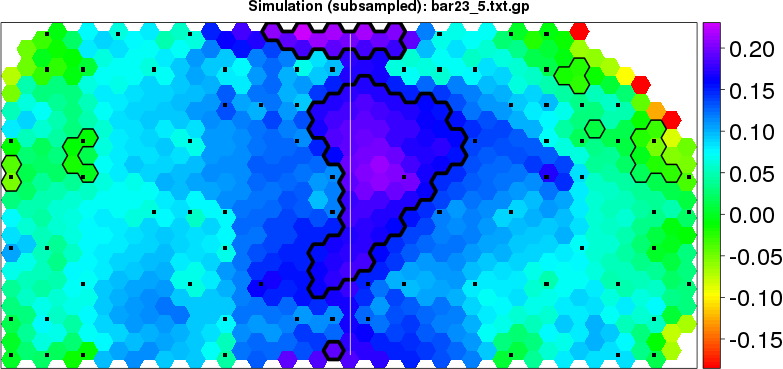 detected=62.9% / unexpected=0.1%
detected=62.9% / unexpected=0.1%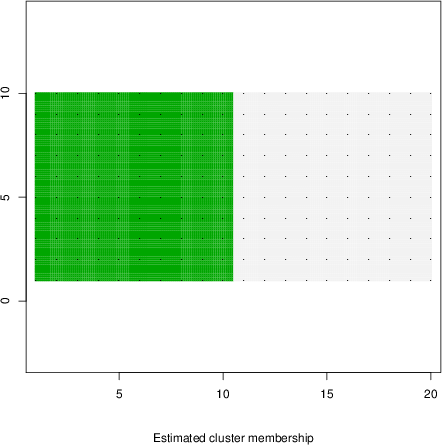
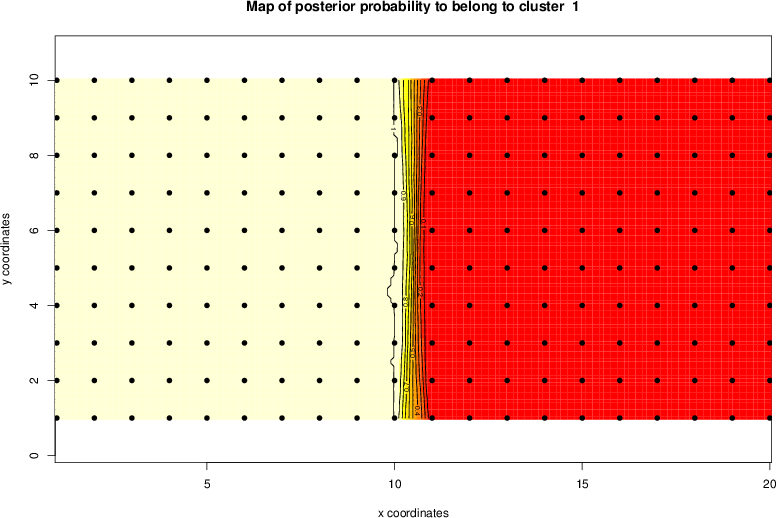
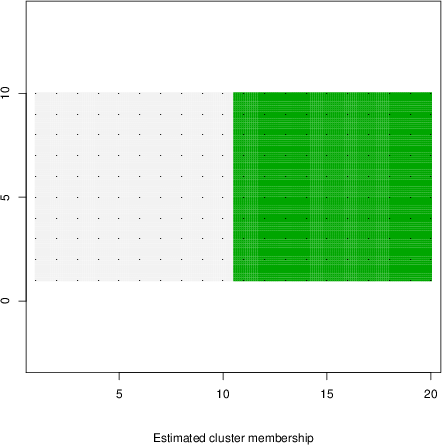
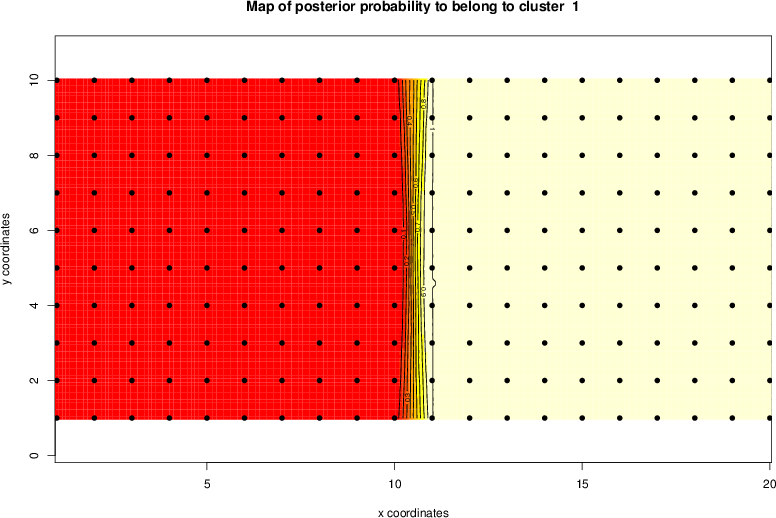
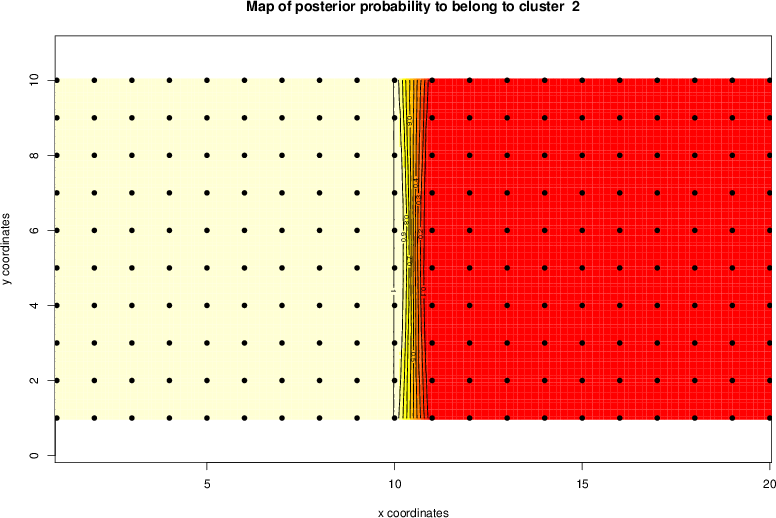
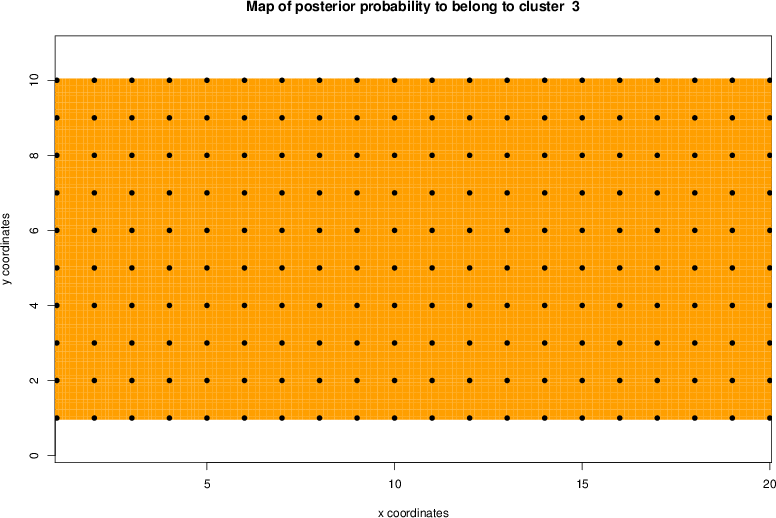
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%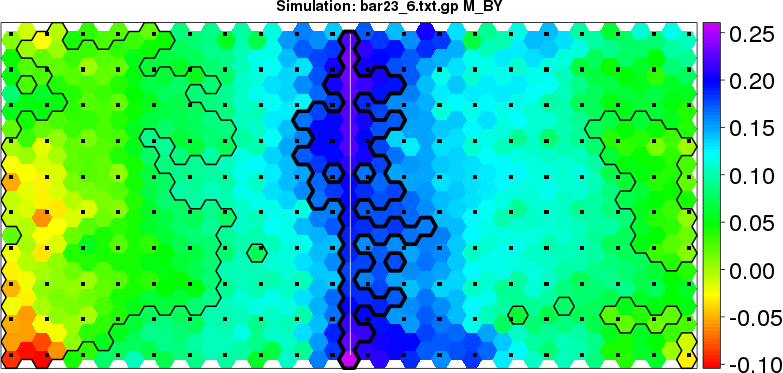 detected=100.0% / unexpected=0.1%
detected=100.0% / unexpected=0.1%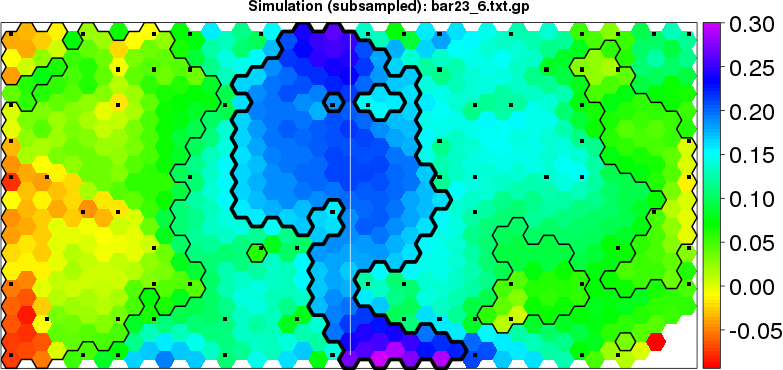 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%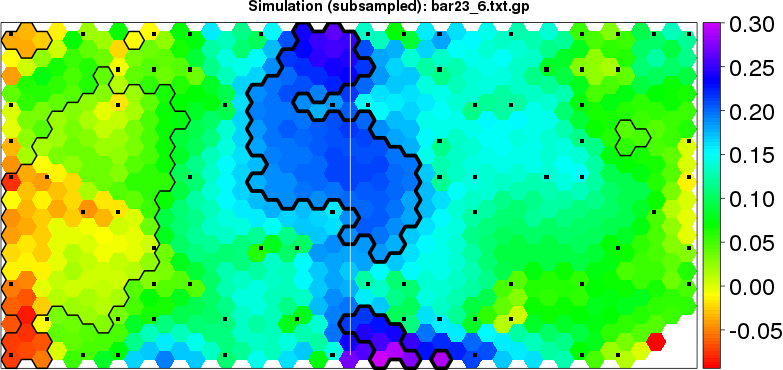 detected=52.3% / unexpected=0.1%
detected=52.3% / unexpected=0.1%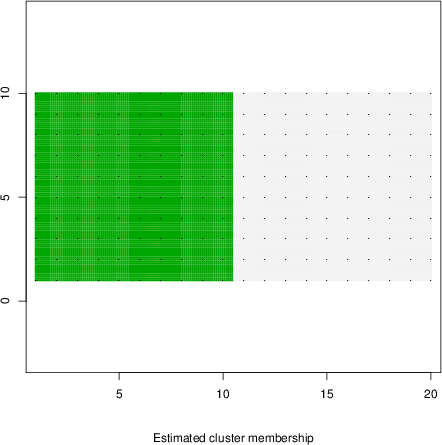
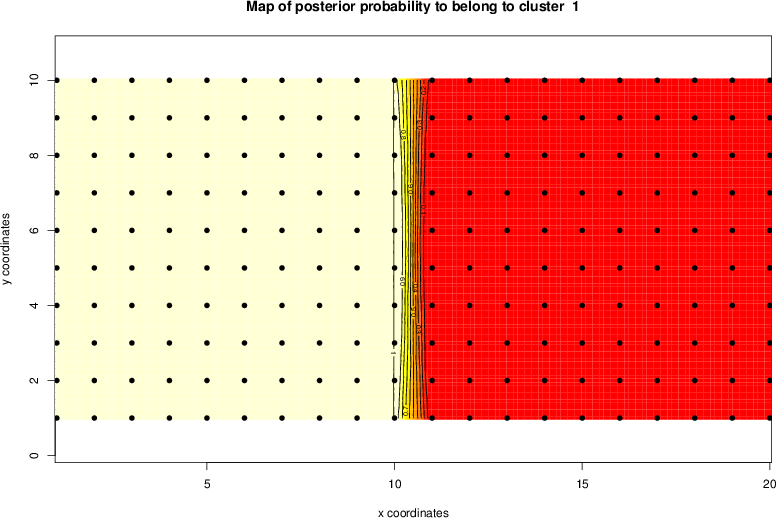
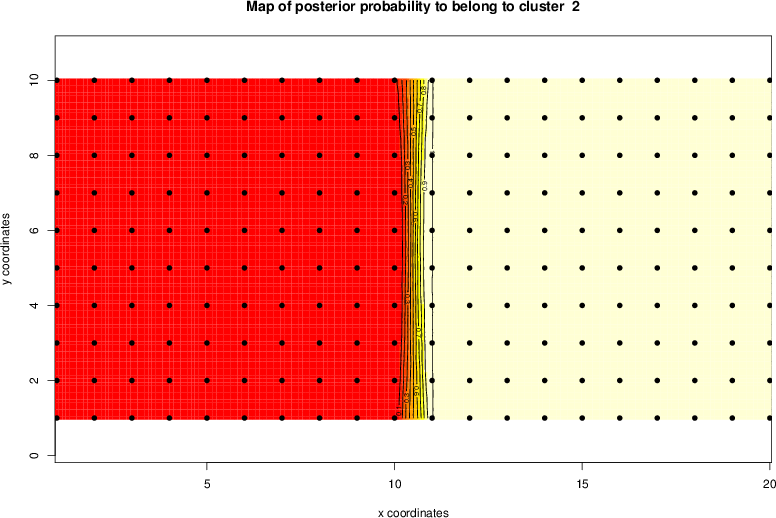
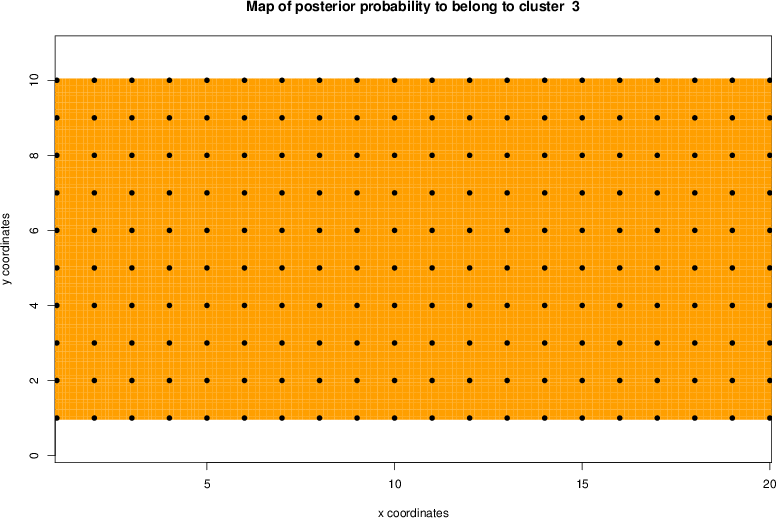
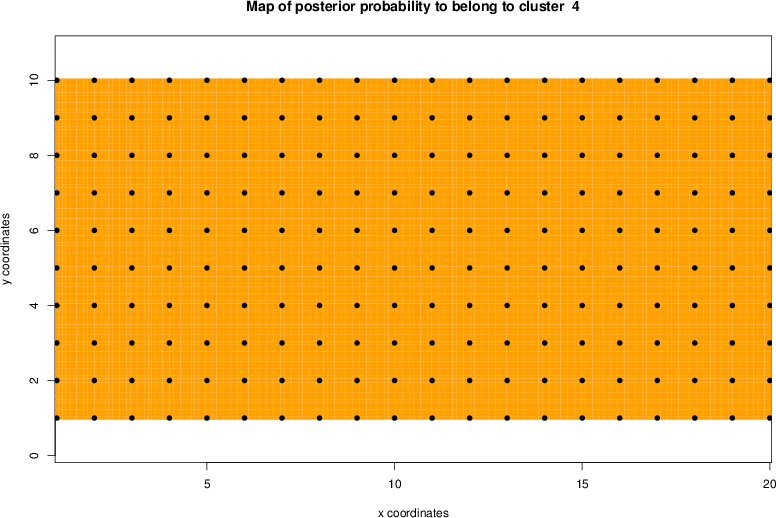
 detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2% detected=90.1% / unexpected=0.2%
detected=90.1% / unexpected=0.2% detected=95.4% / unexpected=1.2%
detected=95.4% / unexpected=1.2% detected=42.4% / unexpected=0.0%
detected=42.4% / unexpected=0.0%
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=90.1% / unexpected=0.1%
detected=90.1% / unexpected=0.1%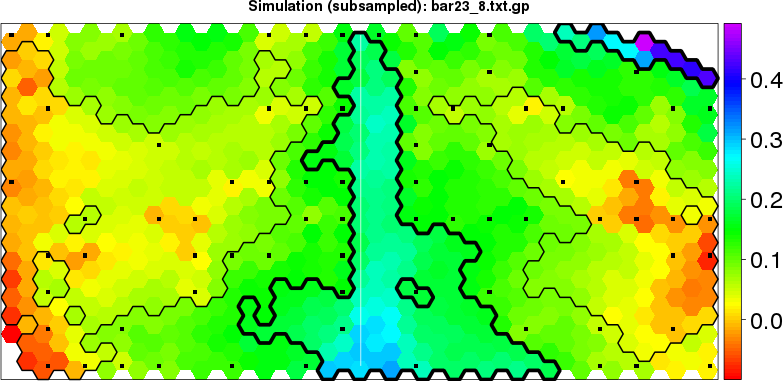 detected=100.0% / unexpected=1.3%
detected=100.0% / unexpected=1.3%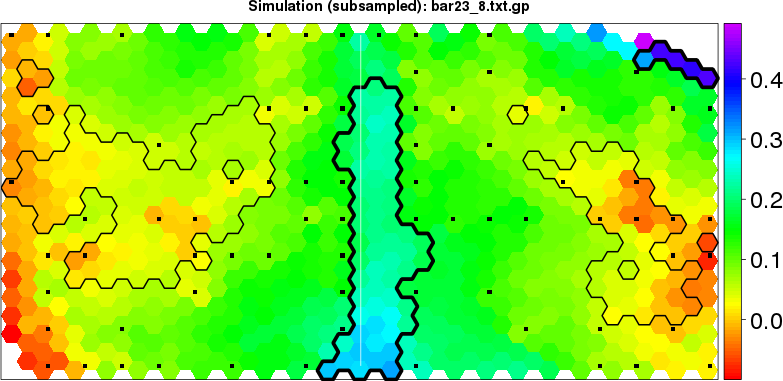 detected=84.8% / unexpected=0.6%
detected=84.8% / unexpected=0.6%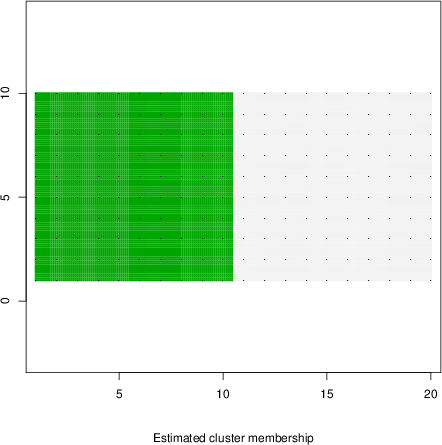
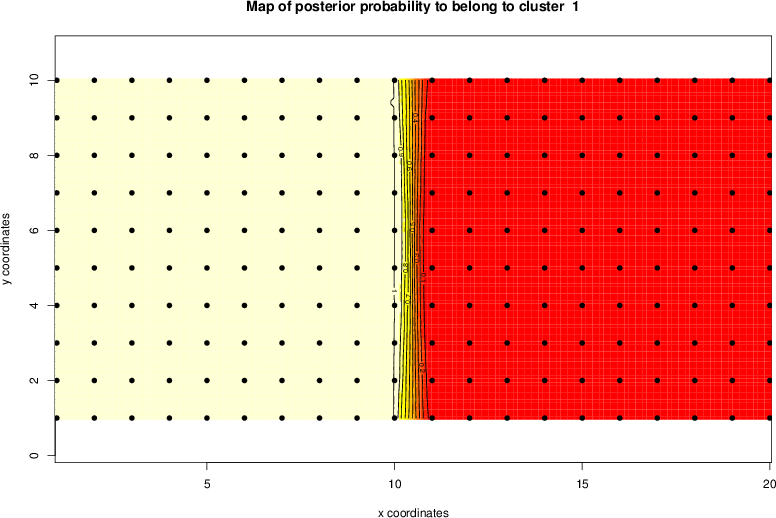
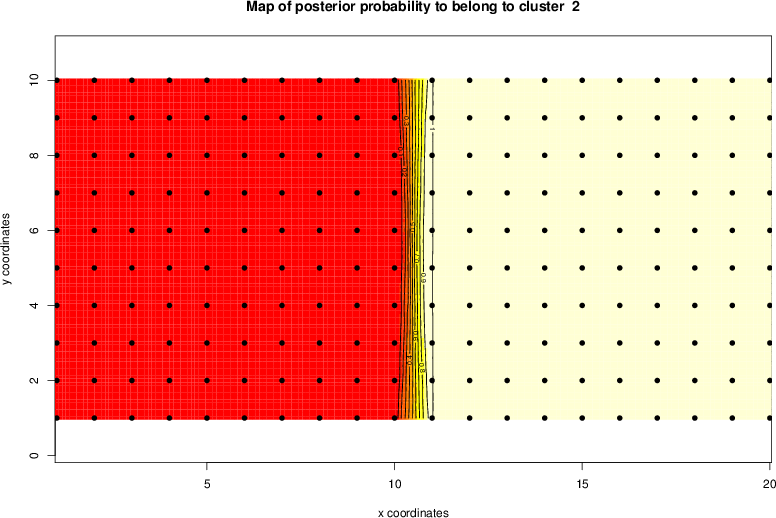
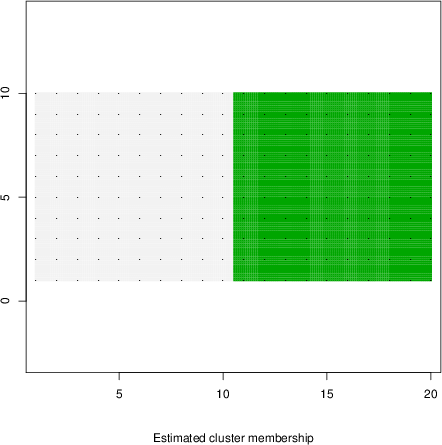
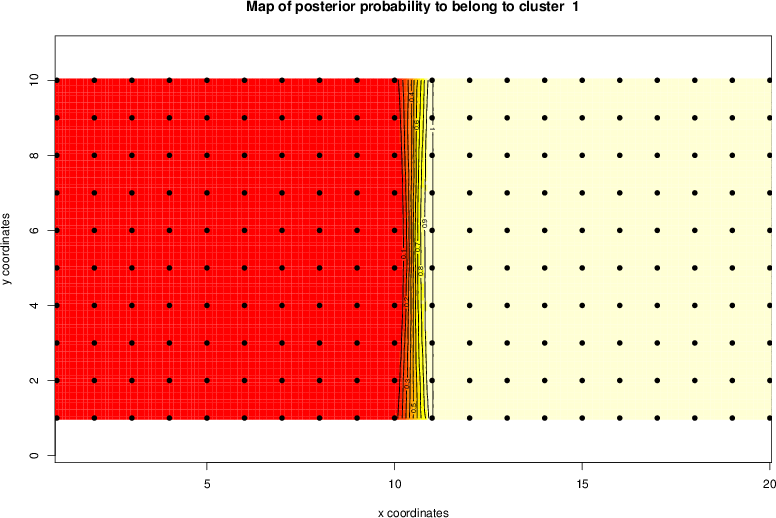
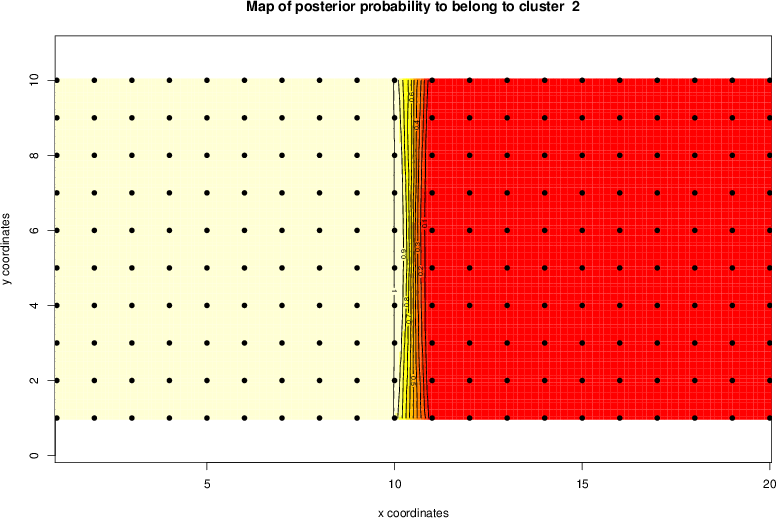
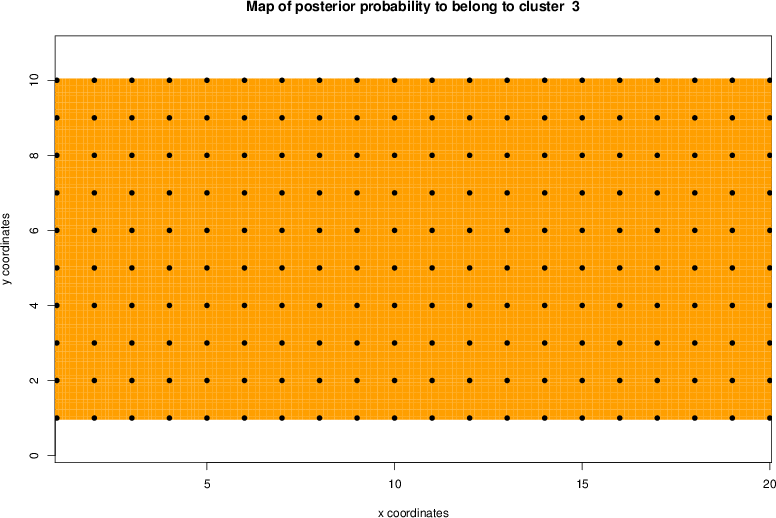
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=95.4% / unexpected=0.2%
detected=95.4% / unexpected=0.2% detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2% detected=84.1% / unexpected=0.0%
detected=84.1% / unexpected=0.0%
 detected=100.0% / unexpected=0.5%
detected=100.0% / unexpected=0.5% detected=89.4% / unexpected=0.1%
detected=89.4% / unexpected=0.1% detected=84.1% / unexpected=0.1%
detected=84.1% / unexpected=0.1% detected=47.0% / unexpected=0.0%
detected=47.0% / unexpected=0.0%
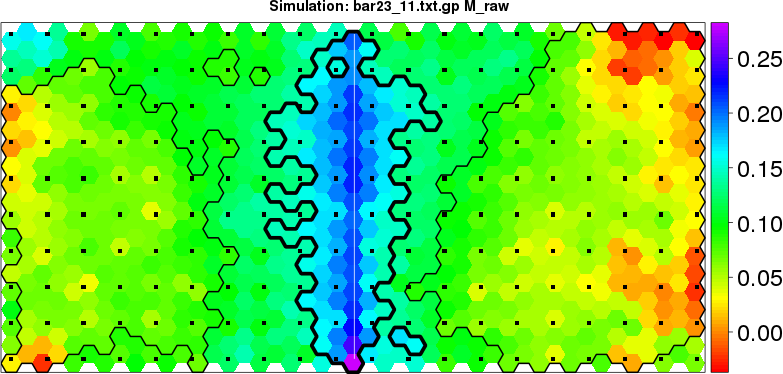 detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2%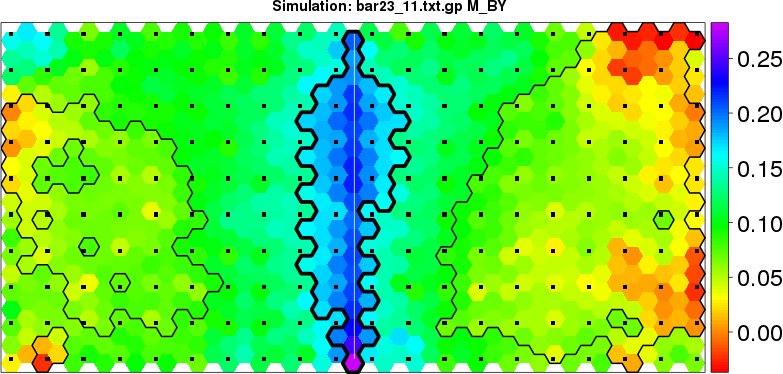 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%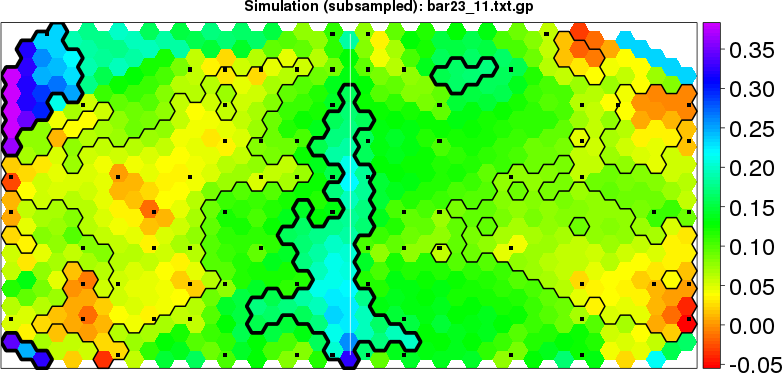 detected=84.8% / unexpected=3.6%
detected=84.8% / unexpected=3.6%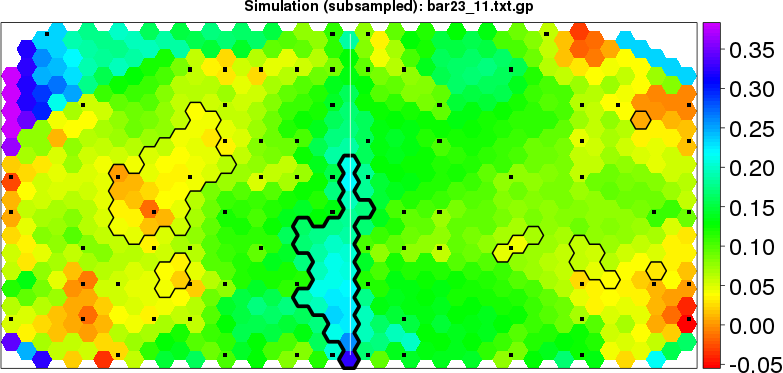 detected=63.6% / unexpected=0.0%
detected=63.6% / unexpected=0.0%
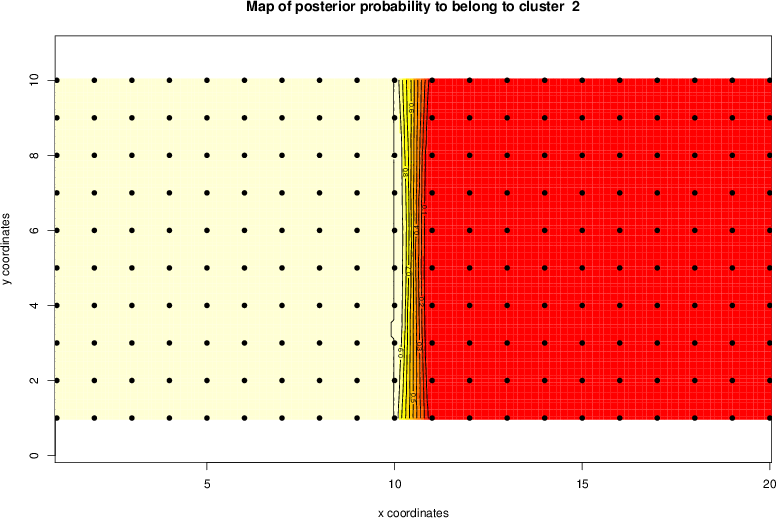
 detected=84.8% / unexpected=0.0%
detected=84.8% / unexpected=0.0% detected=74.2% / unexpected=0.1%
detected=74.2% / unexpected=0.1%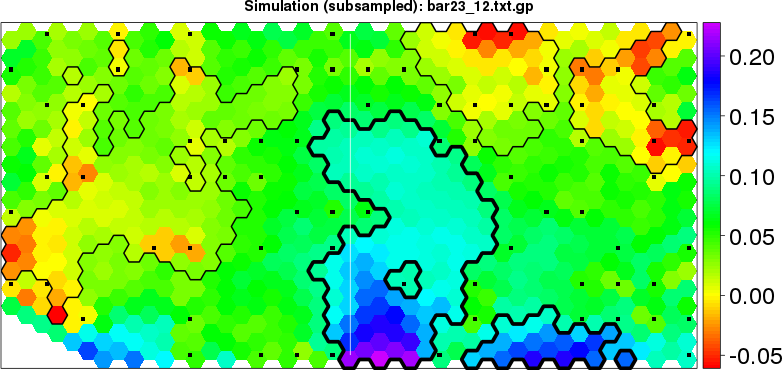 detected=63.6% / unexpected=2.5%
detected=63.6% / unexpected=2.5%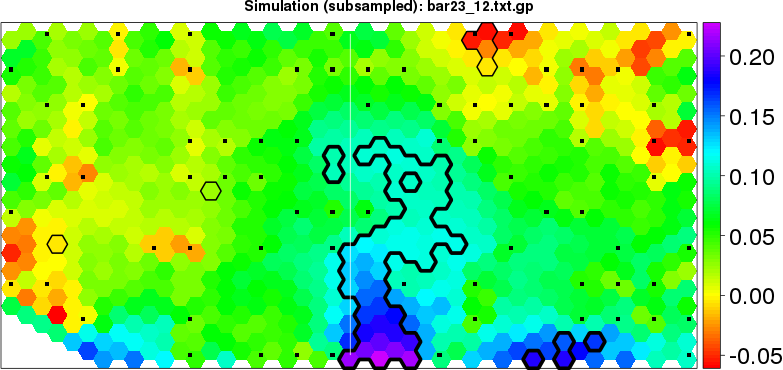 detected=21.2% / unexpected=0.7%
detected=21.2% / unexpected=0.7%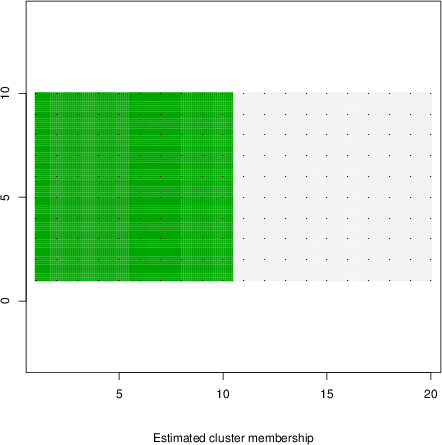
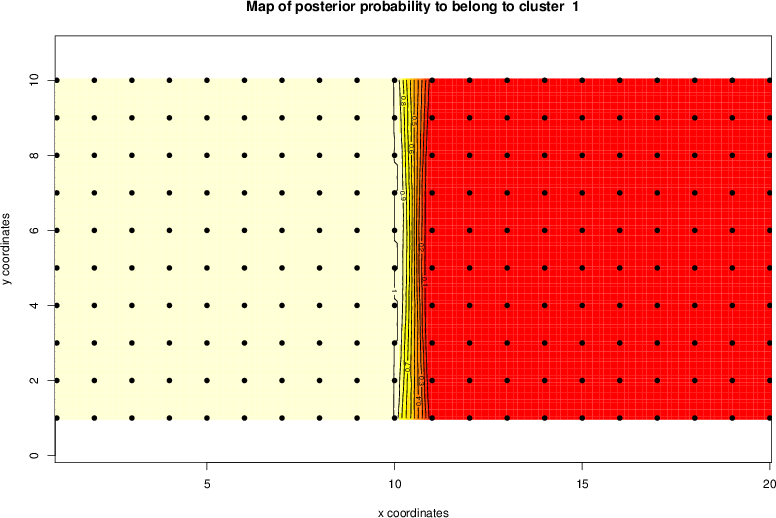
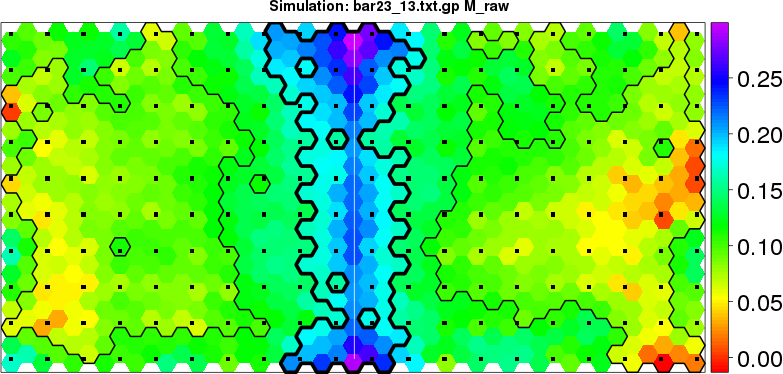 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%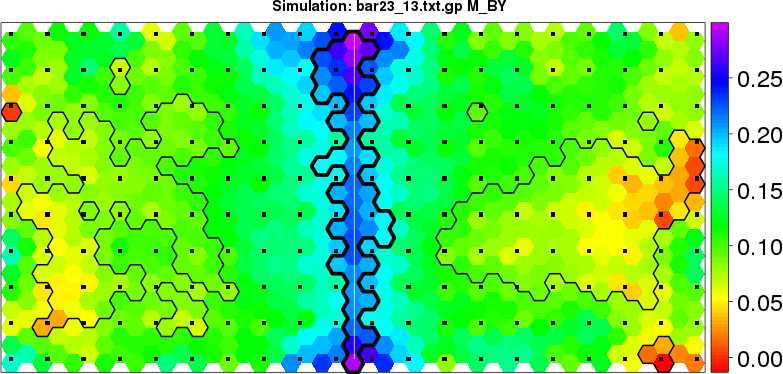 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%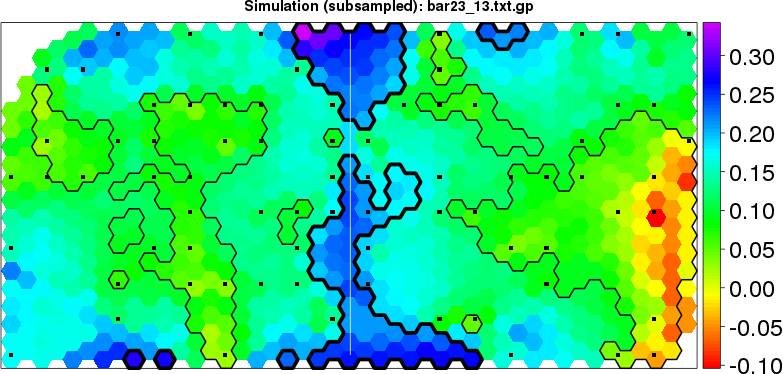 detected=89.4% / unexpected=0.7%
detected=89.4% / unexpected=0.7%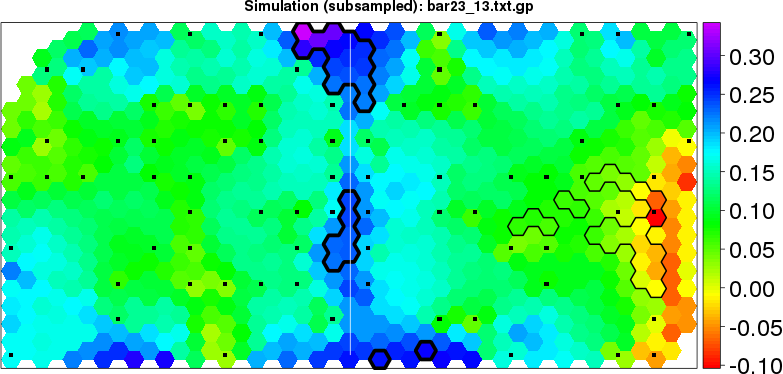 detected=36.4% / unexpected=0.2%
detected=36.4% / unexpected=0.2%
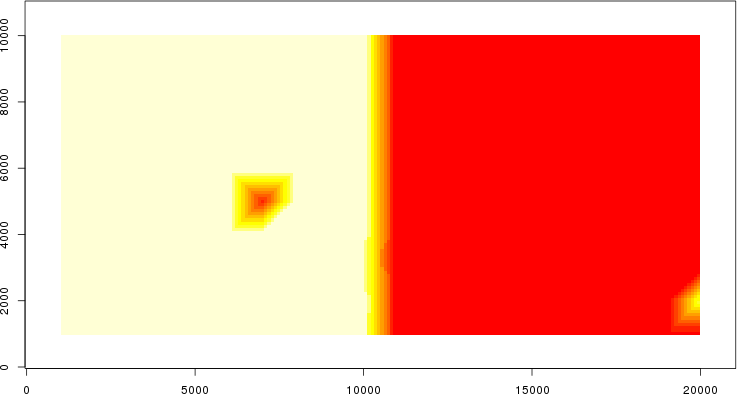
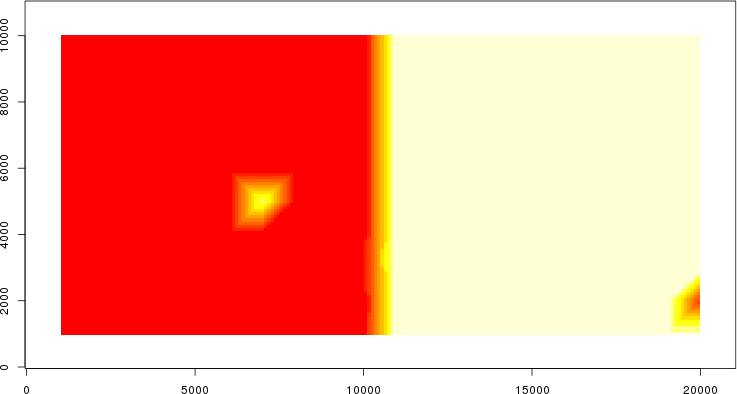
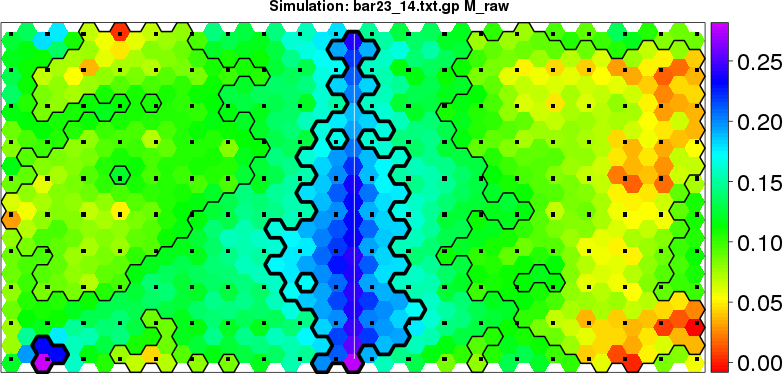 detected=100.0% / unexpected=0.4%
detected=100.0% / unexpected=0.4%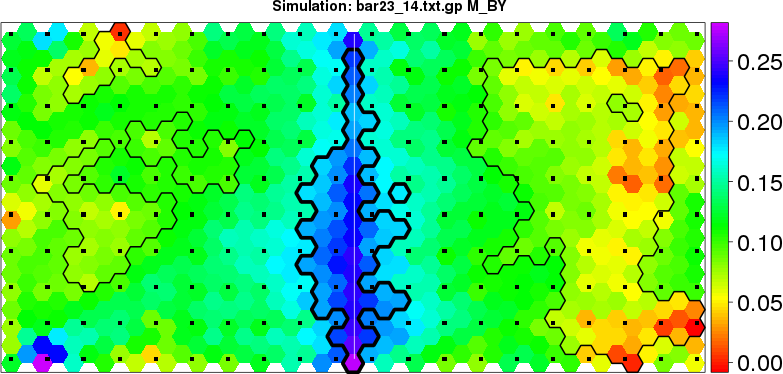 detected=95.4% / unexpected=0.1%
detected=95.4% / unexpected=0.1% detected=78.8% / unexpected=1.7%
detected=78.8% / unexpected=1.7% detected=31.8% / unexpected=0.1%
detected=31.8% / unexpected=0.1%
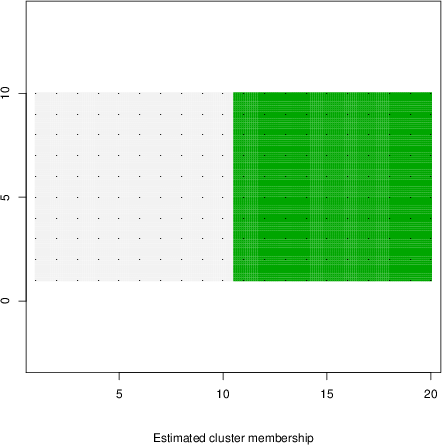
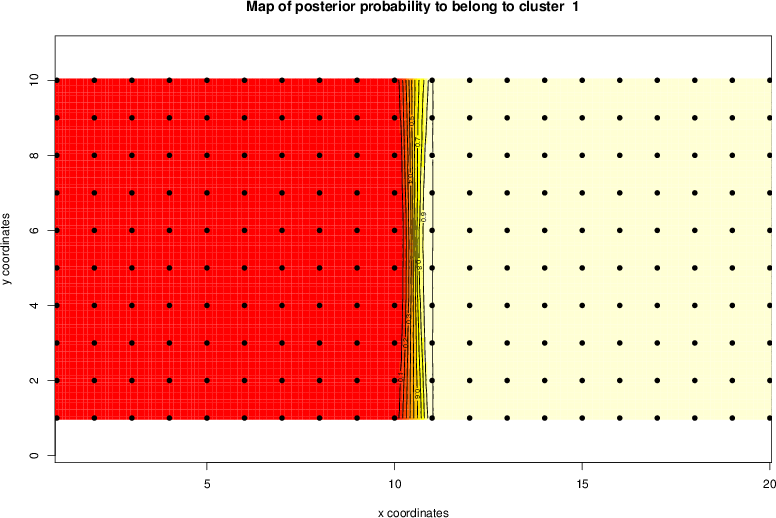
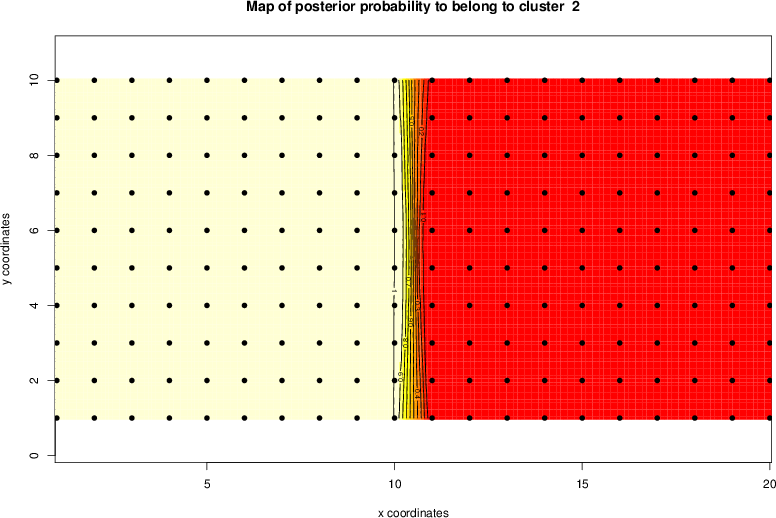
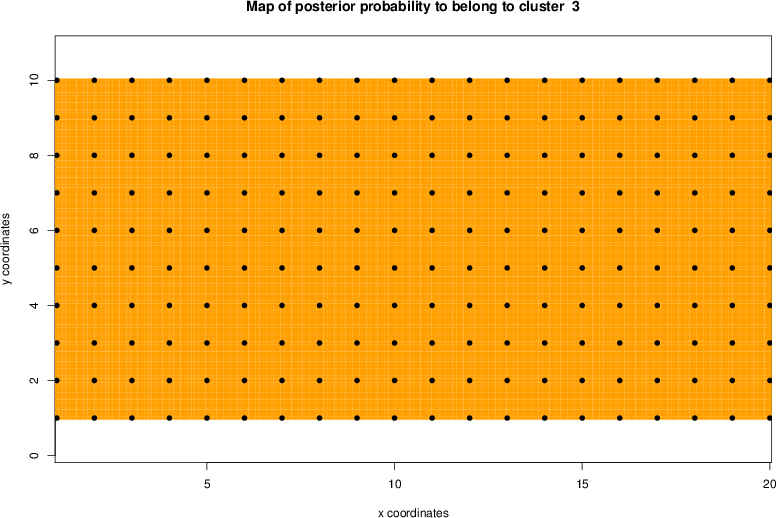
 detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2% detected=95.4% / unexpected=0.0%
detected=95.4% / unexpected=0.0% detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=84.8% / unexpected=0.1%
detected=84.8% / unexpected=0.1%
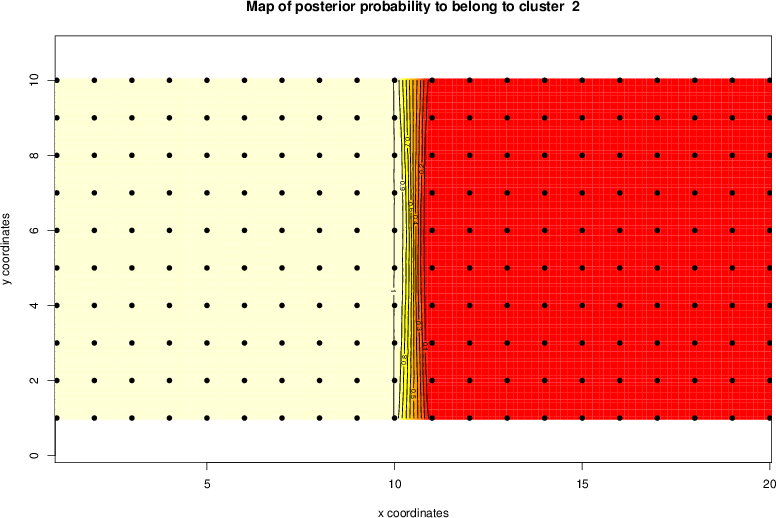
 detected=100.0% / unexpected=0.1%
detected=100.0% / unexpected=0.1% detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=1.5%
detected=100.0% / unexpected=1.5% detected=79.5% / unexpected=1.1%
detected=79.5% / unexpected=1.1%
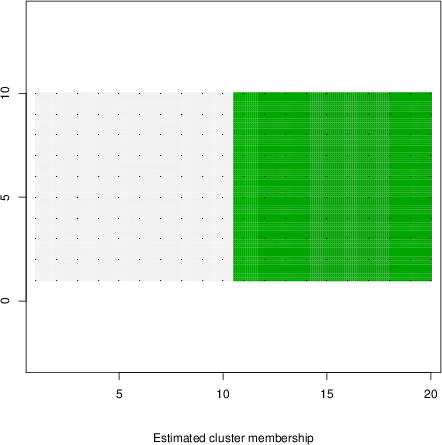
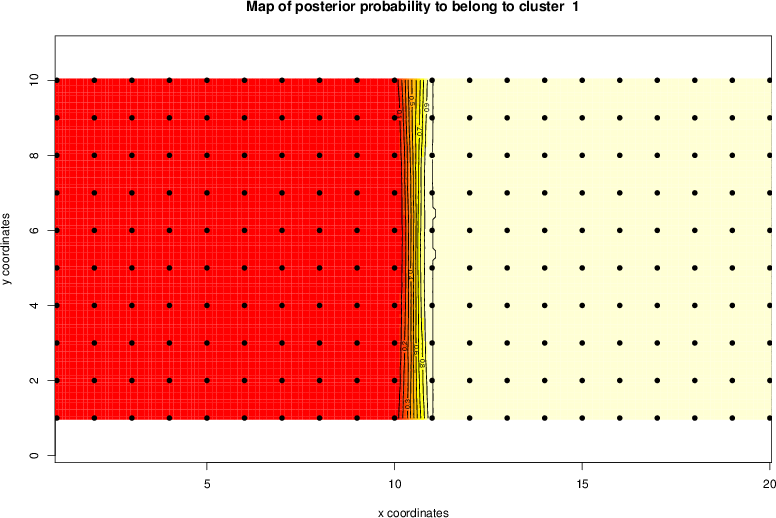
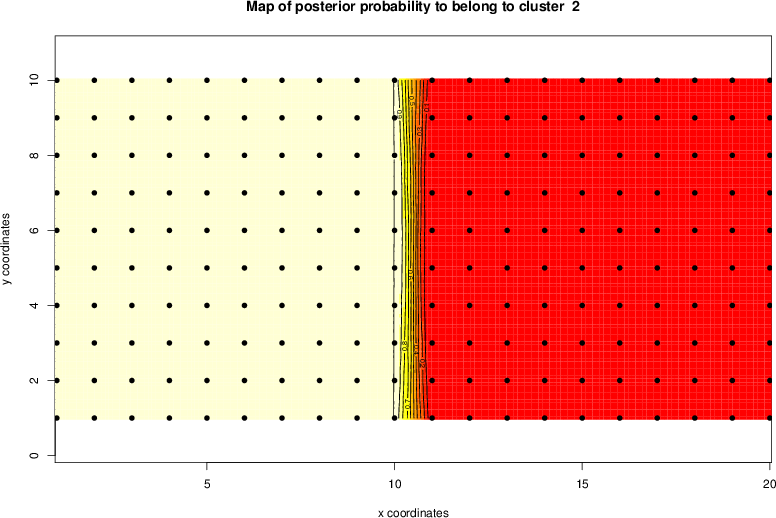
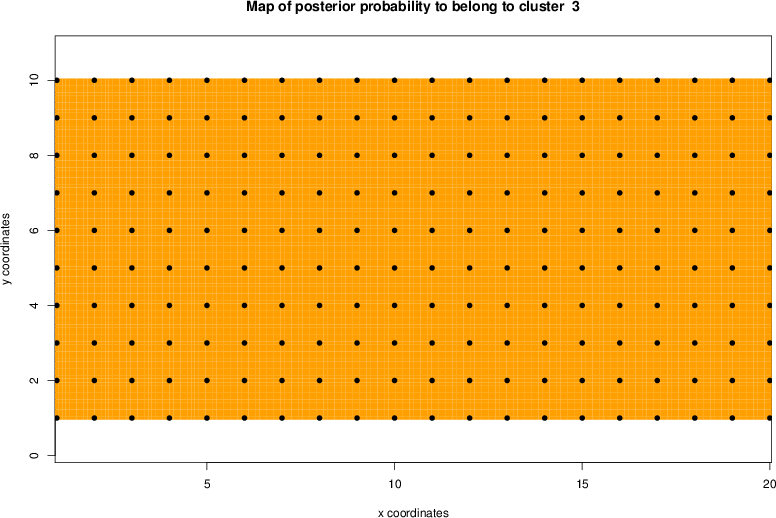
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=95.4% / unexpected=0.1%
detected=95.4% / unexpected=0.1% detected=63.6% / unexpected=0.1%
detected=63.6% / unexpected=0.1%
 detected=100.0% / unexpected=0.1%
detected=100.0% / unexpected=0.1% detected=90.1% / unexpected=0.0%
detected=90.1% / unexpected=0.0% detected=84.8% / unexpected=0.0%
detected=84.8% / unexpected=0.0% detected=53.0% / unexpected=0.0%
detected=53.0% / unexpected=0.0%
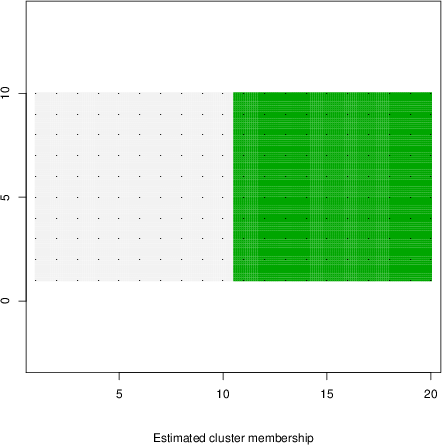
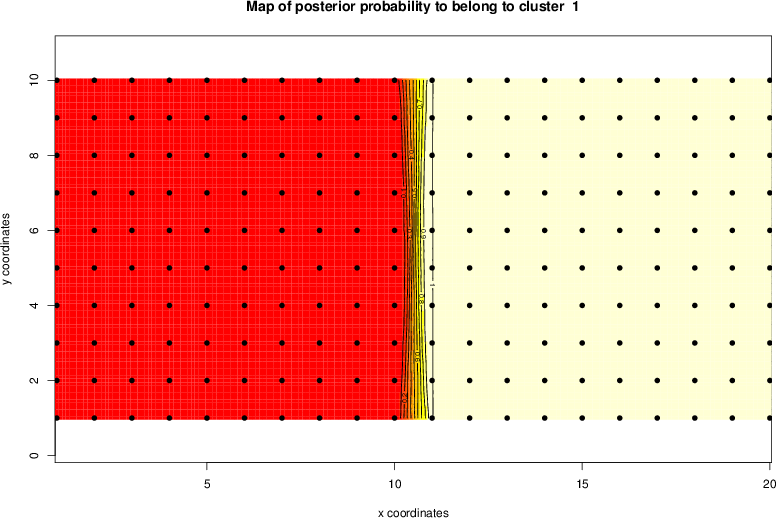
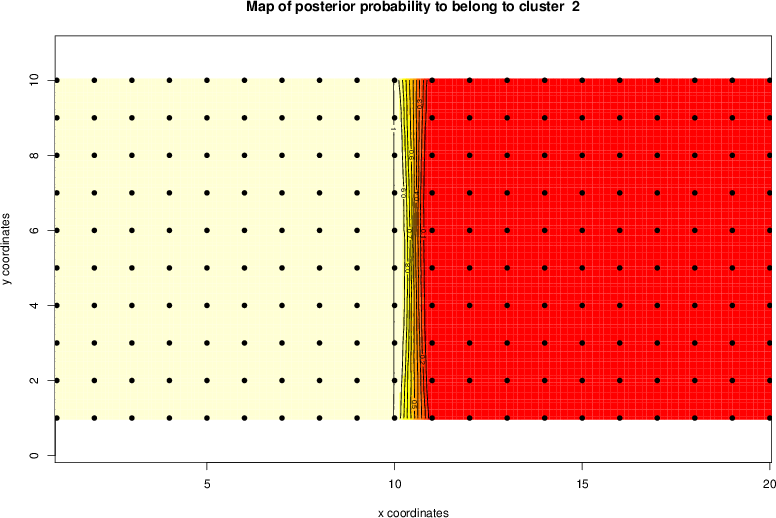
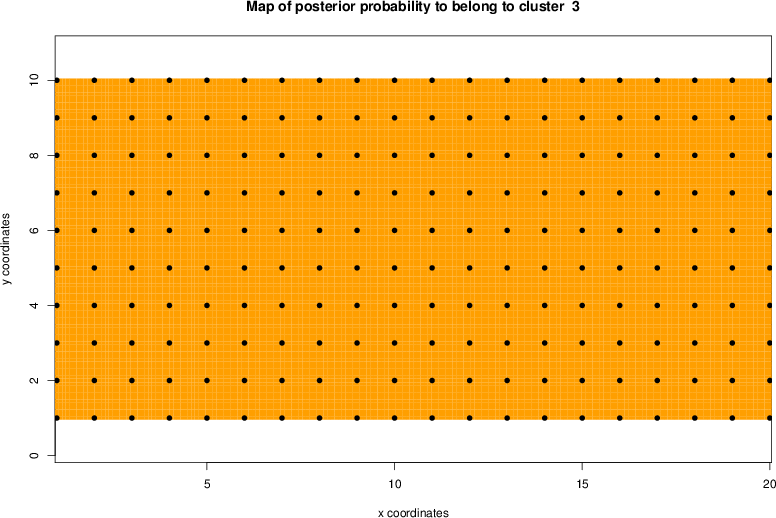

 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=0.4%
detected=100.0% / unexpected=0.4% detected=90.1% / unexpected=0.8%
detected=90.1% / unexpected=0.8% detected=84.8% / unexpected=0.1%
detected=84.8% / unexpected=0.1%
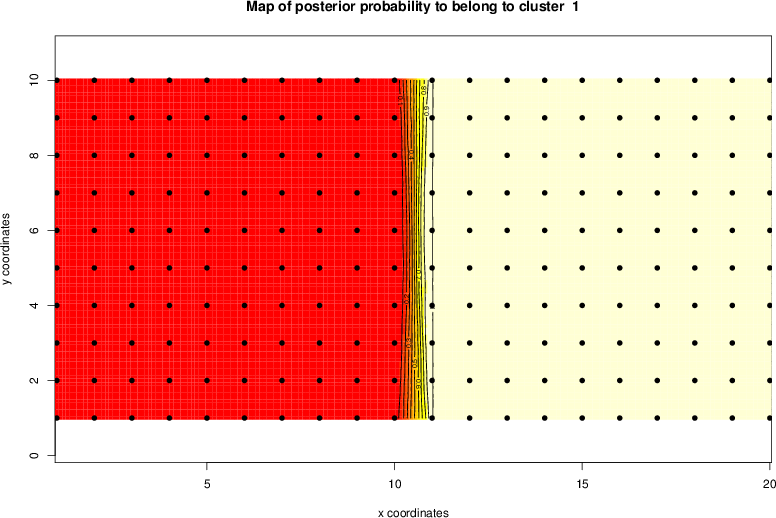
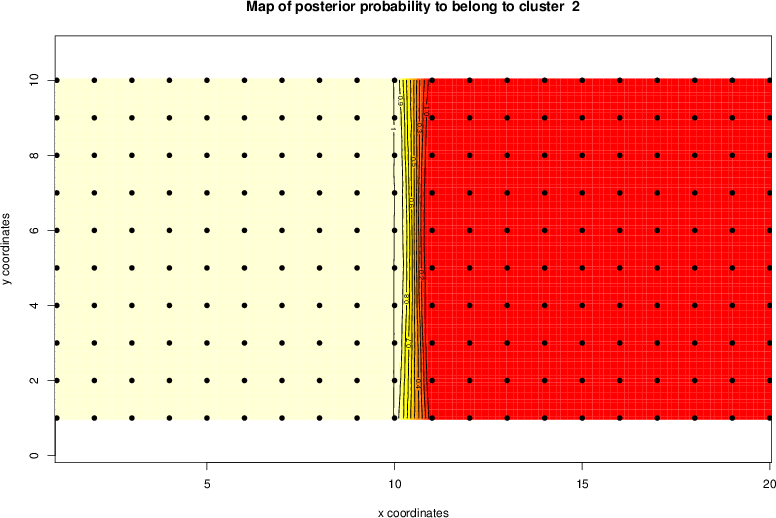
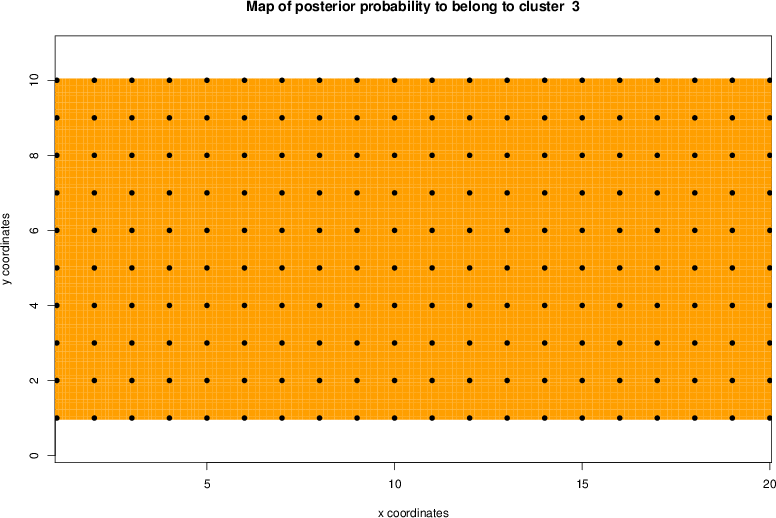
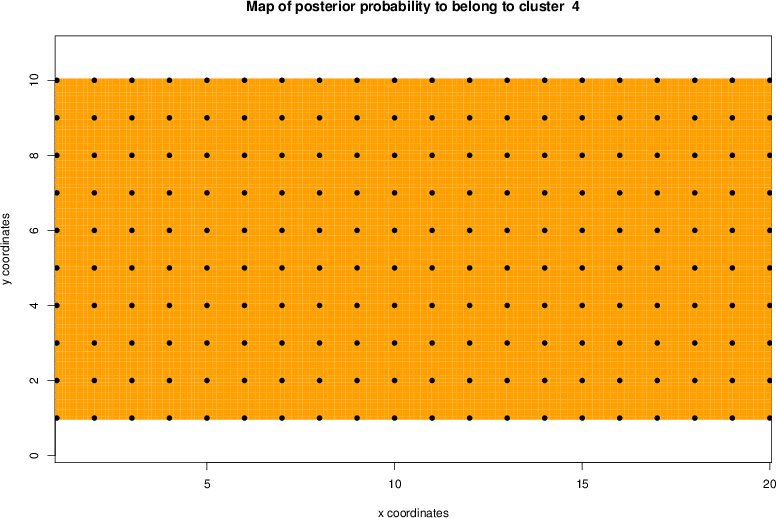
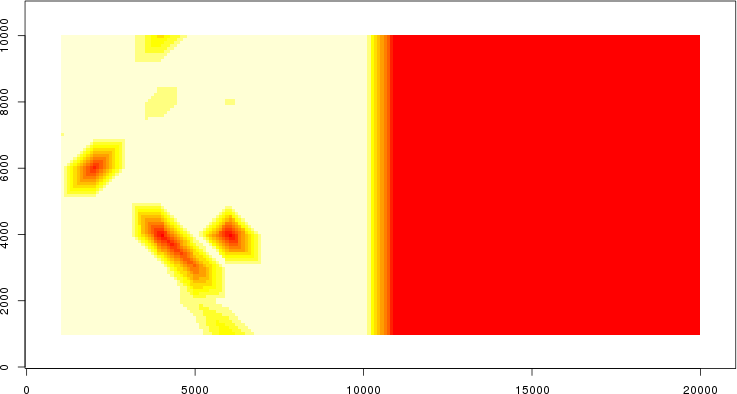
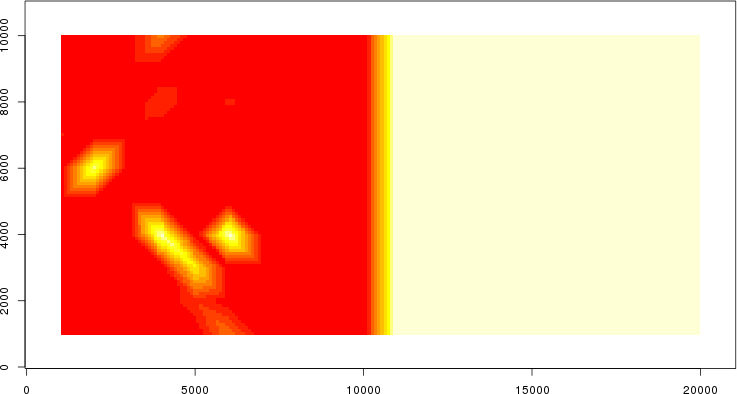
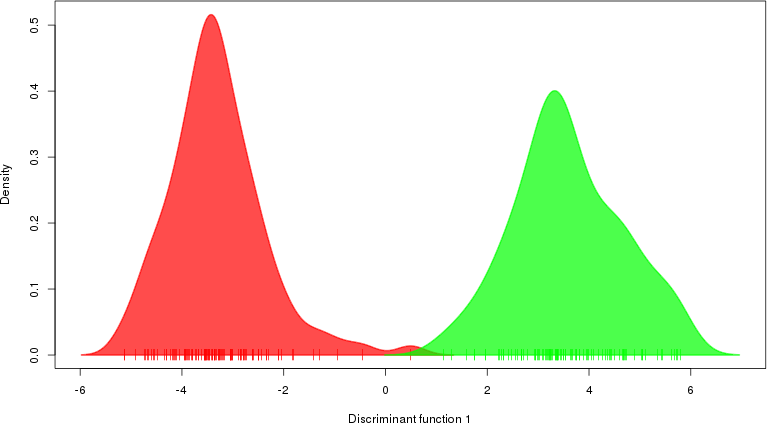
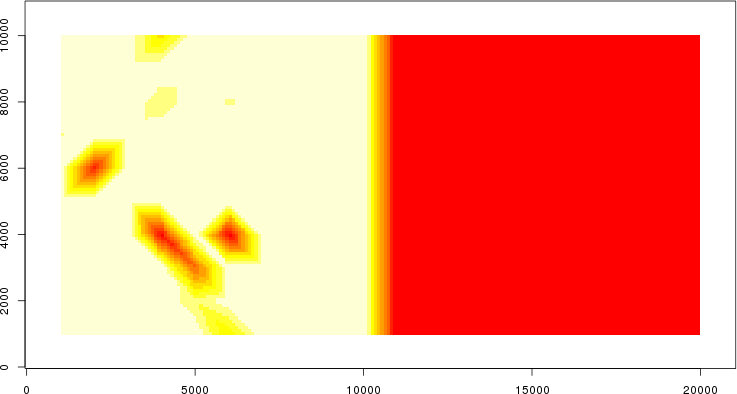
 detected=100.0% / unexpected=0.4%
detected=100.0% / unexpected=0.4% detected=79.5% / unexpected=0.0%
detected=79.5% / unexpected=0.0% detected=84.8% / unexpected=1.3%
detected=84.8% / unexpected=1.3% detected=63.6% / unexpected=0.0%
detected=63.6% / unexpected=0.0%
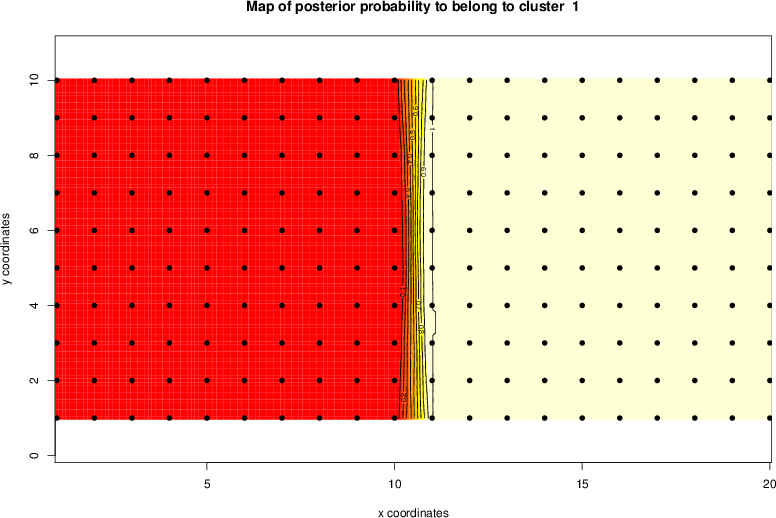
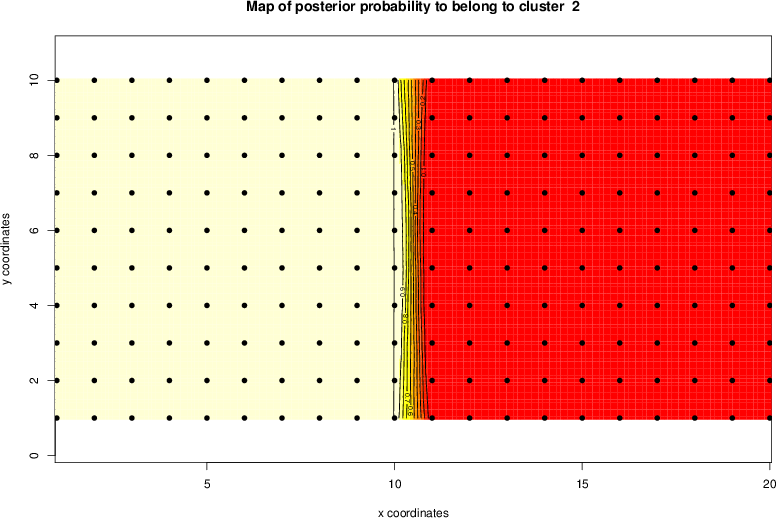
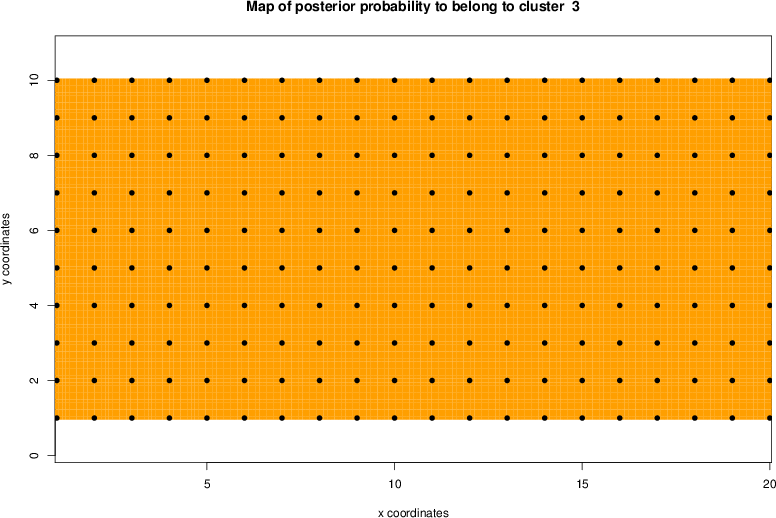
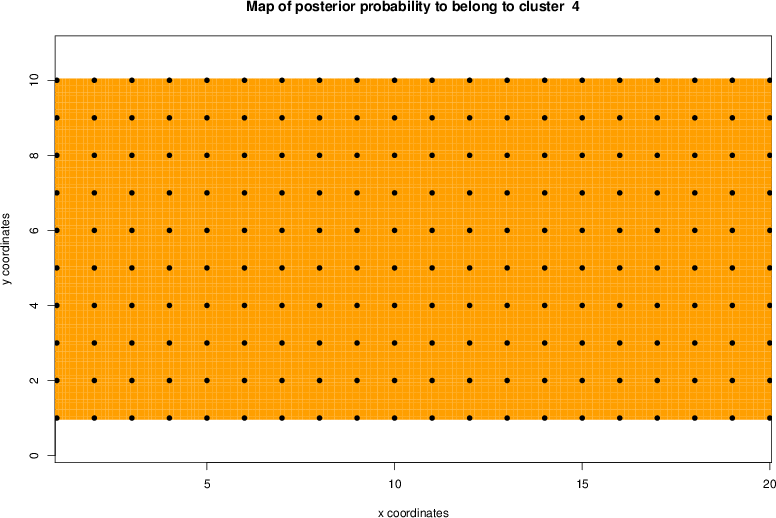
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=0.1%
detected=100.0% / unexpected=0.1% detected=74.2% / unexpected=0.2%
detected=74.2% / unexpected=0.2%
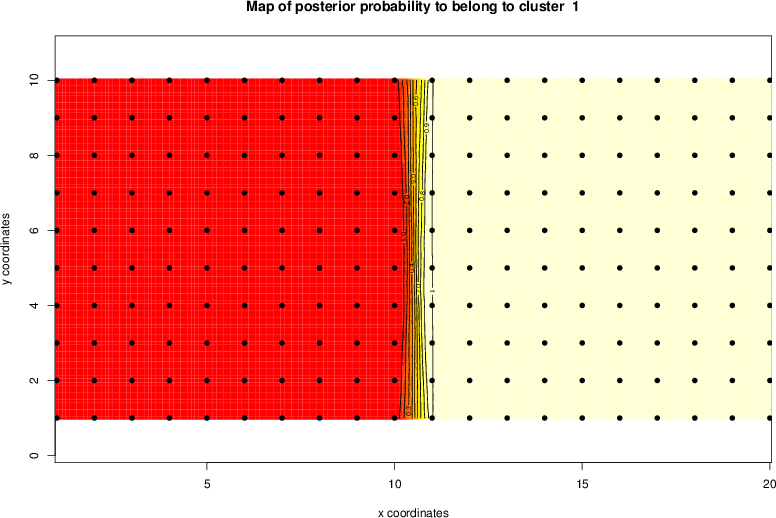
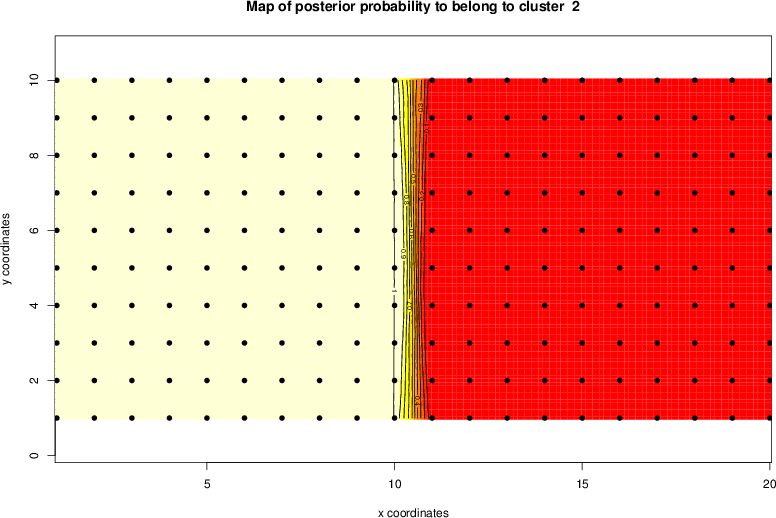
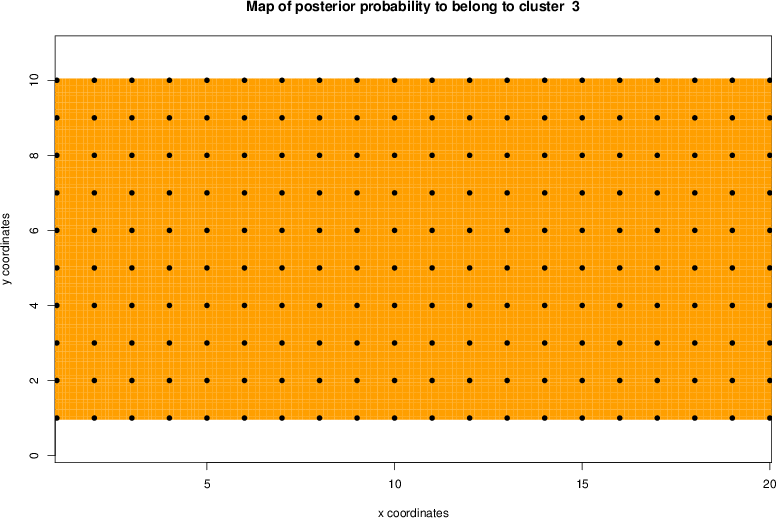
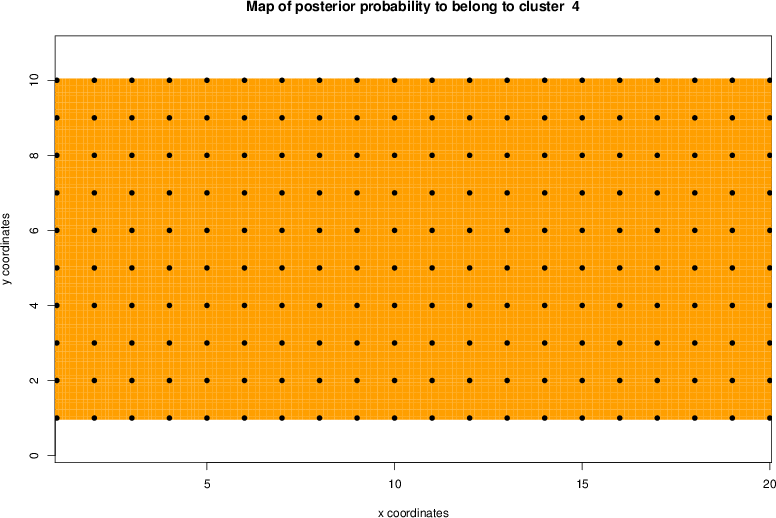
 detected=95.4% / unexpected=0.0%
detected=95.4% / unexpected=0.0% detected=90.1% / unexpected=0.1%
detected=90.1% / unexpected=0.1% detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2% detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%
 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0% detected=100.0% / unexpected=0.1%
detected=100.0% / unexpected=0.1% detected=100.0% / unexpected=0.1%
detected=100.0% / unexpected=0.1% detected=84.1% / unexpected=0.0%
detected=84.1% / unexpected=0.0%
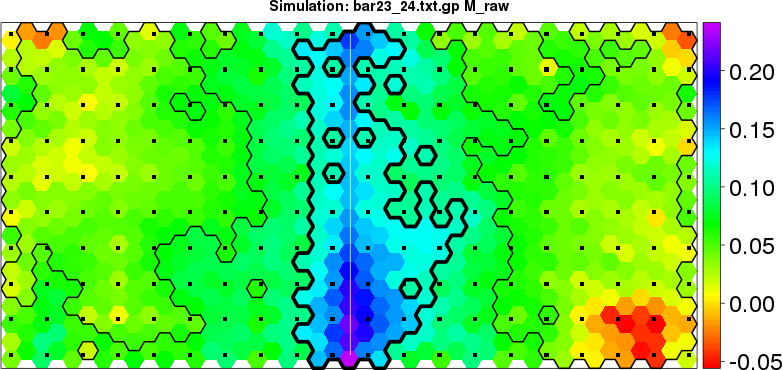 detected=100.0% / unexpected=0.2%
detected=100.0% / unexpected=0.2%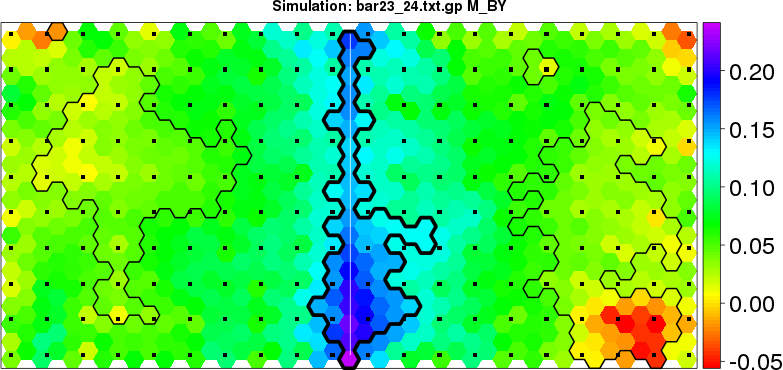 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%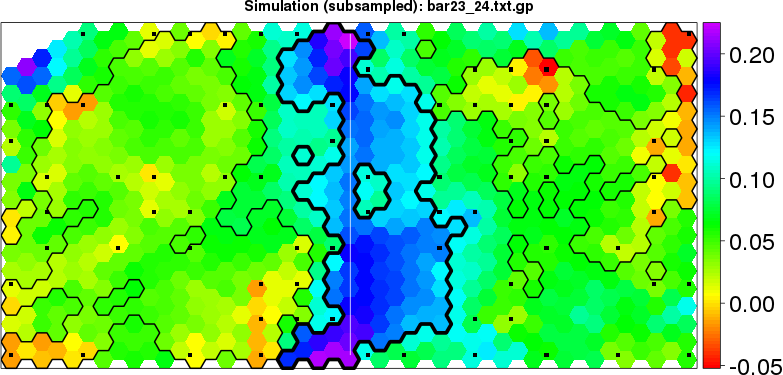 detected=100.0% / unexpected=0.1%
detected=100.0% / unexpected=0.1%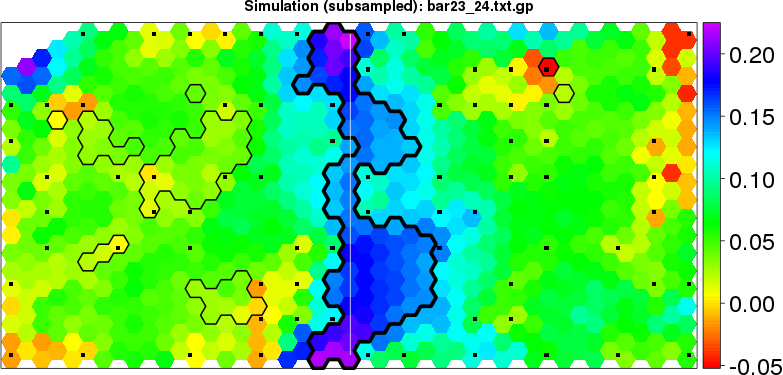 detected=94.7% / unexpected=0.0%
detected=94.7% / unexpected=0.0%
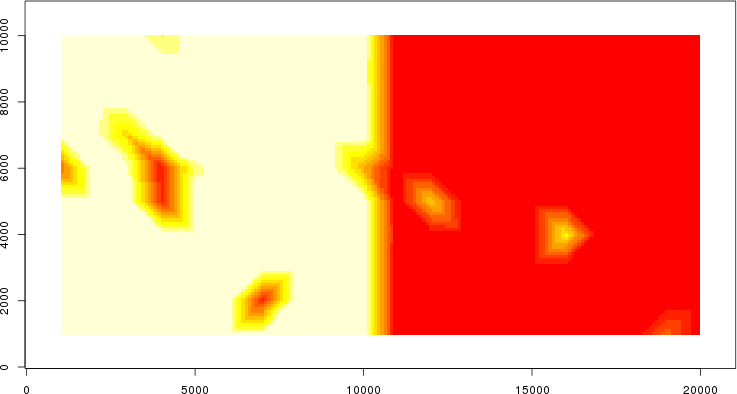
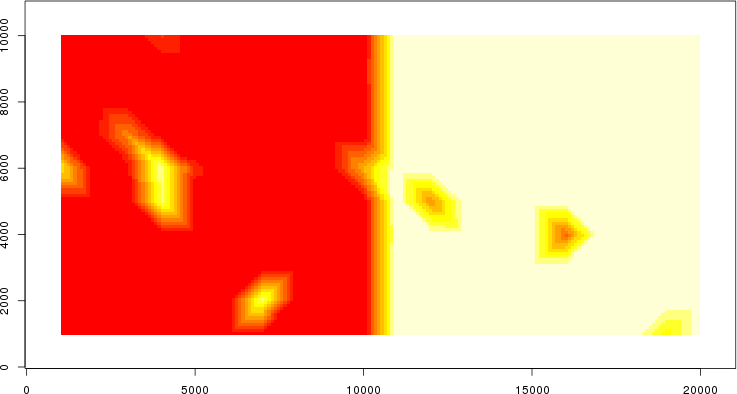
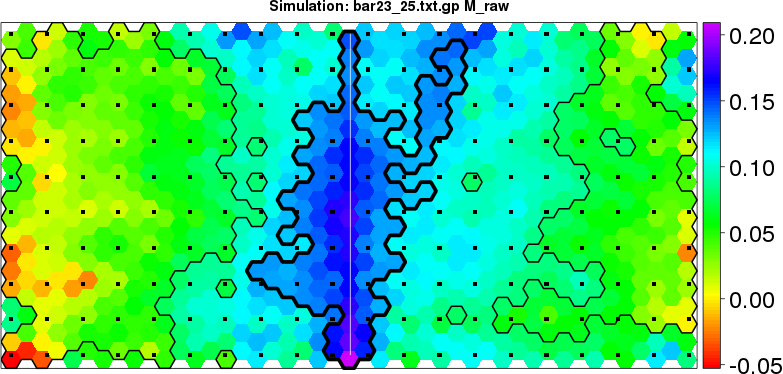 detected=100.0% / unexpected=0.0%
detected=100.0% / unexpected=0.0%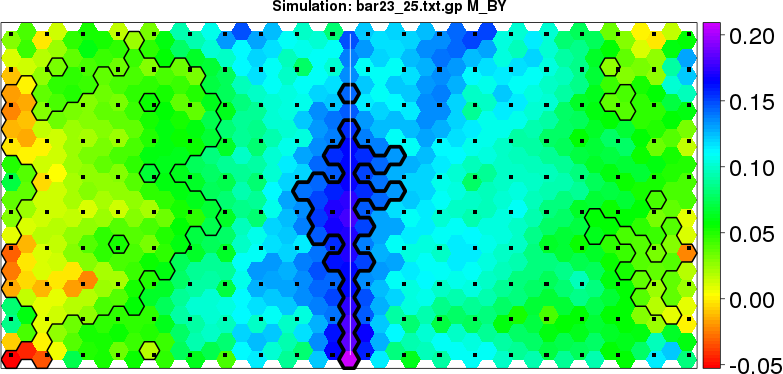 detected=79.5% / unexpected=0.0%
detected=79.5% / unexpected=0.0% detected=84.1% / unexpected=0.1%
detected=84.1% / unexpected=0.1% detected=37.1% / unexpected=1.2%
detected=37.1% / unexpected=1.2%