Bowman, Clive ¹

¹✉ Mathematical Institute, University of Oxford, Oxford, OX2 6GG, United Kingdom.

2023 - Volume: 63 Issue: Suppl pages: 4-16

Proceedings of the 9^th Symposium of the EurAAc, Bari, July, 12^th–15^th 2022

Keywords

Abstract

Introduction

Three free-living astigmatid mite species can be found co-occurring in UK beehives: Carpolyphus lactis (Linnaeus) (Carpoglyphidae), Glycyphagus domesticus (De Geer) (Glycyphagidae), and Tyrophagus putrescentiae (Schrank) (Acaridae). In terms of comparative idiosomal size across a wide variety of free-living forms, Bowman (2021c) categorised all three of these as having an interstitial, potential cavity-living habit. Zoology is beset by'just-so stories' whereby observational claims are made in support of various philosophies. As Akimov (1985) outlines, mite cheliceral chelae as tools differ in gross form, which may or may not be related ecomorphologically to particular lifestyles. What is crucially important in accepting any such explanations is that quantitatively they make sense. That is, the physical working of features is numerically consilient with any posed function. As Gebeshuber and Gordon (2011) says: ''... biologists have changed, and the way they approach their science is getting closer and closer to the world of engineers, in terms of concepts, language and methods''.

Robaux et al. (1977) reported T. putrescentiae to be an excavating geophage. The question arises that if all free-living astigmatids use their cheliceral chelae to do such digging, how big a bite could each species take? Furthermore, for any of an interstitial, potential cavity-living habit, how long is such a mite likely to take to dig out a hole large enough to hide in? This requires one to estimate: the span (i.e., the effective gape) of a maximally open chela, the size of the mastication surface with which the moveable digit rests upon any material and generates friction, and the bite size when a moveable digit surface grasps into material. A check will also be made that variation in these parameters is consilient with previous attribution of feeding design using the ontology of Fashing (1998) and thus if the three co-occurring species could avoid trophic competition by mechanical design.

Material and methods

Preserved slide material of independently determined C. lactis, G. domesticus and T. putrescentiae collected from a single hive habitat in Redland, Avon, BS6 7JP, UK in 1983 deposited at Pest Infestation Control Laboratory, Slough was accessed by the author totalling 52 female specimens. Individuals of: C. lactis were ''with sticky wetness'' on 9^th April, G. domesticus were ''on surfaces'' on 9^th and 10^th April, and T. putrescentiae were ''under propylis/wax'' on 10^th April, all in the bee-nest (= brood box).

Drawings of each mite and its chelicerae (and for T. putrescentiae the lengths of its D1, D2 and L2 idiosomal setae) were made from all cleared mounted specimens using Nomarski interference phase-contrast microscopy with a drawing tube and micrometer scale. Idiosomal index (Lynch 1989) in µm was measured throughout and denoted IL. The lengths of dorsal setae (D1, D2, L2 – Griffiths et al. (1990)) were measured in µm for T. putrescentiae in order to determine Don Griffiths' likely breeding group using the classifier from Bowman (2021b). Tyrophagus putrescentiae'B' is now assumed to be almost certainly the less commonly occurring close relative Tyrophagus fanetzhangorum Su et al., 2020, but definitive identification of voucher specimens already deposited in museums (see Acknowledgments in Bowman (2021c)) is awaited. Tyrophagus putrescentiae'A' (the'commonly occurring form') retains its original name in this investigation following Klimov and OConnor (2009, 2010, 2015) and is not renamed as Tyrophagus communis Fan et Zhang, 2007. Individuals denoted as'B' or'A/B' (i.e., those individuals when the classifier based upon setal lengths on one side of the mite disagreed with the conclusions for setal length on the other side) were excluded from the analysis as mixed populations in the'wild' may occur (Erban et al. 2016).

Drawings were scanned using a HP OfficeJet Pro 8720 and digitised measurements of: IL, setal lengths D1, D2 and L2; chelal design (L1U, L2M, CHI, CLI following (Bowman 2021c); and, cheliceral dentition [x,y] profiles with respect to the condyle-to-tip L2M axis were made using ImageJ 1.51s ex National Institutes of Health USA (available from http://imagej.nih.gov.uk/ij ). Mite chelae were orientated by reflection and rotation such that their adductive lever moment arm directions (i.e., L2M see Bowman (2021c)) were aligned. Two fixed homologous features (the moveable digit tip and the fixed digit to moveable digit articulating condyle) were used for registration (Figure 1) i.e., the L2M axis is the'reference line'. One landmark, the moveable digit tip, labeled (1) plus seventeen semi-landmarks (labeled 2–18) were determined by first scaling each L2M axis to the same size (rooted on the condyle) and then overlaying a equi-spaced 2D grid in order to digitise the moveable digit profile (black line in Figure 2) at standard increments along the L2M axis. Semi-landmark 18 was that directly vertical above the centre of the condyle seen laterally. This was not necessarily exactly where the adductive tendon inserts into the'coronoid process' of the moveable digit (that is the length of y₁₈ after undoing the rescaling does not necessarily match L1U). The moveable digit tip was taken to be the origin i.e., [x=0, y=0]. It is understood that a grid space of 1 indicates a slightly different actual spacing in µm for different specimens, but this is not about defining universal landmarks rather it is to deploy digit length adjusted semi-landmarks comparable across chelal designs.

Analyses were done in Excel2011 and R version 3.4.4 (2018-03-15) using untransformed data. Heat-maps and 3D plots used Graphis 2.7.3. Illustrations of the physics involved use the larger female Tyrolichus casei (Oudemans) cheliceral chela for clarity of exposition.

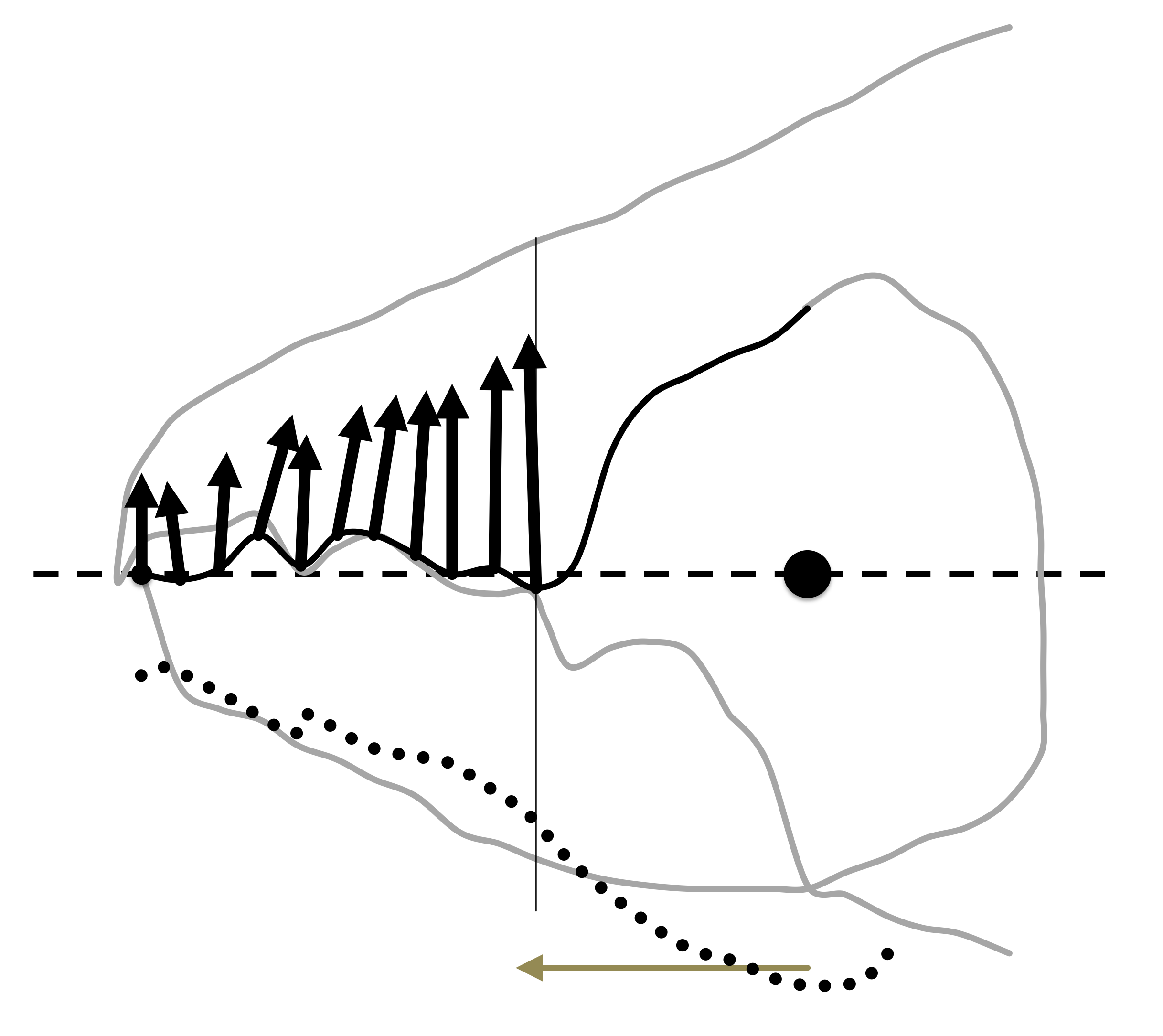
Chelal velocity ratio

The velocity ratio (= the ideal mechanical advantage) at the cheliceral chelal tip of the moveable digit (VR_tip) was calculated as \(\frac{L1U}{L2M}\) (i.e., the length of the input moment arm divided by the length of the output moment arm of the closing adductive lever (Bowman 2021a)). No adjustment for adductive tendon angle was made.

End of mastication surface

The start of the chelal mastication surface, was taken to be the tip of the moveable digit, [x₁,0]. Jerk along the profile [x,y], i = 1...18 was estimated by

\[\frac{d^3 y}{dx^3} = \frac{c_{i+1}-c_{i-1} }{x_{i+1}-x_{i-1} }, i = 4...15\]

where

\[c_i = \frac{d^2y}{dx^2} = \frac{g_{i+1}-g_{i-1} }{x_{i+1}-x_{i-1} }, i = 3...16\]

and

\[g_i = \frac{dy}{dx} = \frac{y_{i+1}-y_{i-1} }{x_{i+1}-x_{i-1} }, i = 2...17\]

The end of the mastication surface \((e)\) equalled that \(x_i\) where \(jerk_i\) or \(c_i\) was at a maximum, given \(y_i\) thereafter was monotonically increasing.

Span of moveable digit

The span of the moveable digit (or maximum effective chelal gape) is that distance from the end of moveable digit mastication surface to the fixed digit tip where any force at the end of moveable digit mastication surface is resisted by the fixed digit tip i.e. \(G = L2M * sin(δ)\). That is, given that the chelal tips meet, it is commensurate with a force orthogonal to L2M being applied (see Figure 1).

Sclerotisation/strengthening

The degree of comparative strengthening by sclerotisation of the condyle and of the moveable digit was scored numerically on a subjective scale (0 = not or feebly sclerotised, 1 = pale but sclerotised, 2 = brown moderately well sclerotised, 3 = dark brown heavily sclerotised) using specimens from Bowman (2021c). Inferred resistive forces at \([x_i , y_i]\) were calculated as \(F1*VR_i\) using F1 values from Bowman (2021c).

Maximum food fragment size grabbed

The difference between the digit tips at the maximum effective gape angle \(δ = cos^{-1}\frac{L2M}{(L2M-x_{ie})}\) in Figure 1 defines the maximum size of a foodstuff fragment that can be grabbed \(= 2*L2M*sin⁡(\frac{δ}{2})\) by the chelal digit tips, together with the consequent minimum fragment size \(= 2*(L2M-x_{ie})*sin(\frac{δ}{2})\) gripped by the end of the moveable digit mastication surface and its opposing fixed digit features proximal to the condyle. Note the maximum size < G always, and the minimum grazes the leading edge of the coronoid process (ascending ramus).

Astigmatid chelicerae work independently, taking it in turns to grab food-stuff and on retraction chopping it either side with the gnathosomal rutella before ingestion. An estimate of food fragment volume Mv_G of a bite or'grab' at the maximum effective gape G (see Figure 1) that could be gripped before any such truncation, would be by taking a cone of 2D apex angle \(δ\) and side length L2M and to subtract away a similar cone of side length \(L2M-x_{ie}\). That is under the Trapezoidal rule, \(= \frac{Π}{3}*(sin(\frac{δ}{2})*\frac{sin(δ)}{2})*(L2M^3-(L2M-x_{ie})^3)\). This is an overestimate as although chelicerae can be approximated as cylinders, the chelal digits themselves are somewhat flattened. It also infers that the lateral truncation of grasped food preferentially occurs distal to the condyle. It represents the maximum chunk that might be torn away by a bite from that mite's single chelicera.

Morsel size pre-ingestion

If the thickness (denoted thick) in μm of chelal digits were known then an estimate of food fragment size after hypostomal truncation (= pre-ingestion morsel size) would be \(= (thick)*\frac{sin(δ)}{2}*x_{ie}*((2*L2M)-x_{ie})\) assuming that the rutella are held running along either side of the digits.

Digit effective thickness might be estimated basally at the condyle (= a constant spacing between the rutellae) or distally at the tip (i.e., the rutellae flexibly press outwards during cheliceral protrusion and then press inwards on retraction so that the minimum gap is the important parameter). Taking the first approach, Mariana et al. (2007) shows a SEM of Blomia tropicalis gnathosoma end-on from the front. From this, the ratio of moveable digit width (basally near the estimated position of the condyle) to cheliceral width (basally) can be estimated as 0.29. This closely agrees with Murillo et al. (2014) where for T. putrescentiae the ratio is approximately 0.28. Using digit thickness at the condyle as indicative of food fragment width after truncation by the rutellae appears reasonable (rather than using the digit width distally) when for instance the magnitude of the intra-pedipalp gap is considered (see gnathosoma of Rhizoglyphus echinopus ventrally in Hammen (1989) illustrated in Wirth (2006)).

Food fragments are dragged alternately by each chelicera into the labral area between the palps. The equivalent ratios for A. siro and A. gracilis in Iraola et al. (2015) were estimated as 0.29 and 0.32 respectively. However, Ahamad et al. (2011) shows an SEM of Suidasia pontifica where this ratio could be estimated somewhat higher at 0.39. Taking the cheliceral digit thickness estimated from various not quite'face-on' scanning electron micrographs of another 46 astigmatid gnathosomal exemplars found on Internet web pages (covering A. siro,'cheese-mite','(house) dust mites', Schwiebia sp., and'unknown') yields an average figure of 0.36. Combining these with the named examples in the above papers yields a consensus estimate of 0.35. This compares favourably with that of the highly derived astigmatids living in water-filled treeholes by Fashing (1998). That paper yields an estimate of 0.37 for Naiadacarus arboricola (although that for Algophagus pennsylvanicus at 0.50 is somewhat higher).

Bowman (2021a) suggests that the width of cheliceral segments are about 0.85 times the height of cheliceral segments i.e., they are sub-cylindrical. Accordingly for this study herein (where CHI was measured on each specimen), moveable digit thickness (thick) is estimated as \(=0.85*0.35*CHI=0.298*CHI\).

Results

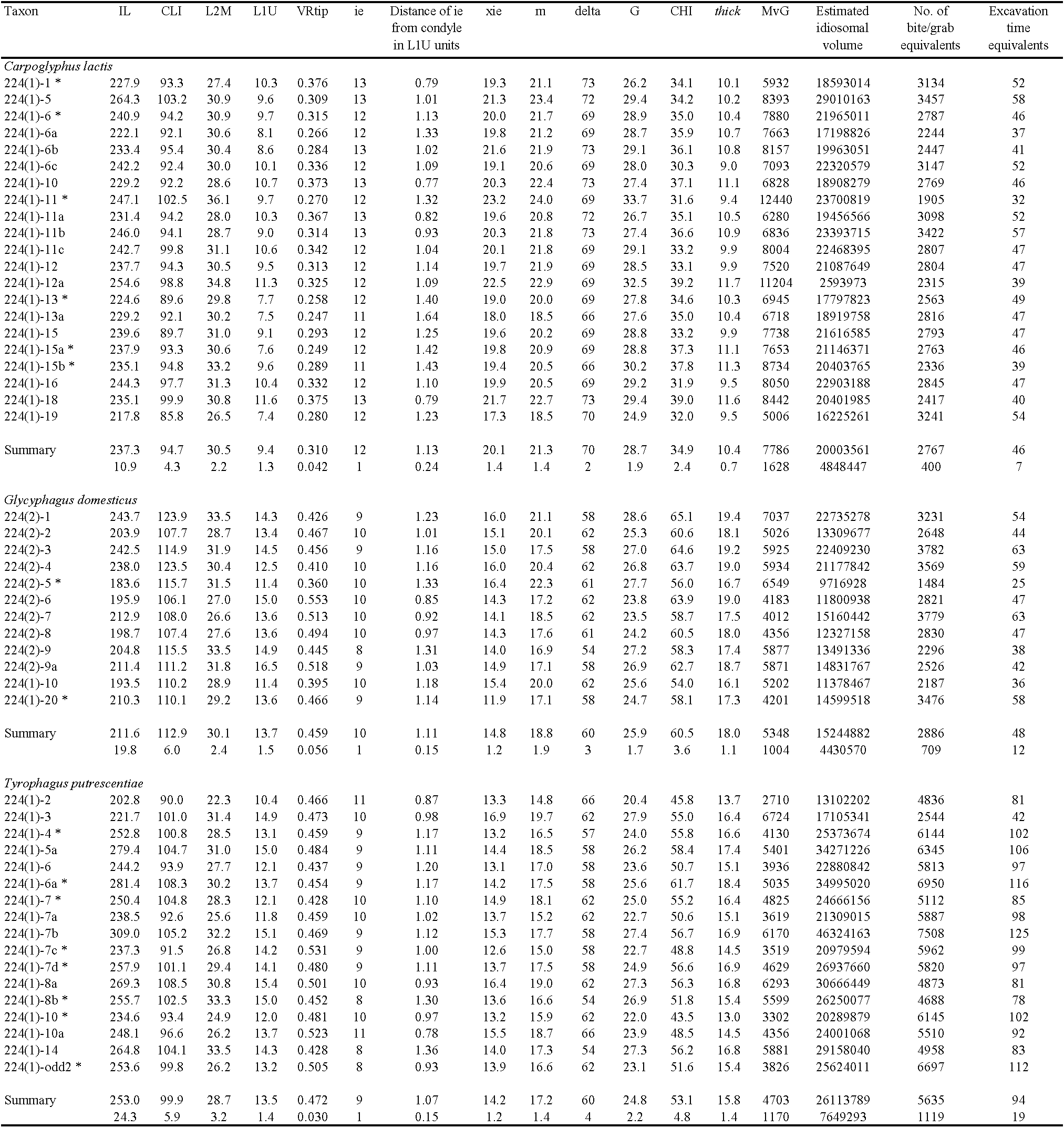
Mean (and sd) values for the lengths in μm of idiosomal setae in the 17 T. putrescentiae female individuals were: D1 43.1 (5.72), D2 127.5 (14.64), L2 43.3 (6.11). Table 1 summarises the chelal results.

Chelal velocity ratio

The wild-collected C. lactis shows the lowest chelal velocity ratio, T. putrescentiae the highest. G. domesticus has the most primitive geometry of its chela in that, unlike the other two species, the attachment point for the adductor tendon with the basal coronoid process of the moveable digit is posterior of the condyle as illustrated for Chortoglyphus arcuatus in Akimov and Gaichenko (1976). This would be an interim state in the evolution of the chela from a simple appendage if it follows the same process as in other jaws (DeMar and Barghusen 1973).

End of mastication surface

The location of maximum jerk on the profile of the chelal moveable digit indicated the end of the mastication surface. In a few mites (marked with *) this was inconsistent and the end of mastication surface was taken to be the semi-landmark before that showing maximum curvature. Overall, the end of the mastication surface is confirmed to be just before the theoretical cut-off point for a functioning chewing'machine' (i.e, where the velocity ratio would be =1).

Span of moveable digit

The largest and smallest span of the moveable digit surface which can grasp material (i.e., the largest and smallest effective gape of a maximally open chela) are respectively, 28.7 μm (C. lactis) and 24.8 μm (T. putrescentiae). Note that although the adductive muscle tendon (inserting around semi-landmark 18 and pulling approximately parallel to L2M axis – would have to flex around it), the coronoid process does not impinge internally upon the dorsum of the chelal shaft. Forces for moveable digit features distal of the end of the mastication surface when maximally open would have no opposition from the fixed digit.

Free-living astigmatids in being saprophagous must be challenged to eat nematodes, nematode eggs, fungal spores and hyphae along with their base foodstuff in the wild (even in beehives). Figure 3 shows values of average x_ie for the wild-collected samples of the three taxa versus the typical sizes for spore, fungal, yeast, plant and animal cells.

Fungal spores vary in general size from 2 to ≈ 100 μm (illustrated in Golan and Pringle (2017)) although some can be as large as 250 μm (Gehring et al. 2002). Most typical soil fungal spores (and even small protists (Luan et al. 2020)) therefore could be grasped by the chela of all three mite species. Fungal (mycorihizal) hyphae are commonly 5−10 μm but can be as small as 3−8 μm in diameter (Dodd et al. 2000). Therefore, the chela of the three UK beehive-living species could grab these too. Note that in extreme cases fungal hyphae can be even as low as 2 μm in size or as large as 1 mm. Protozoa, rotifers, tardigrades and nematodes are 4−200 μm in size meaning that some of these could be grasped (even anecdotally) by these astigmatids. Soil nematodes are non-segmented worms typically 50 μm (range 15–100 μm) in diameter. Some of these (< 20 μm diameter) could be grasped by the scale of mastication surfaces in the three UK beehive species. Entomophagous nematodes are known to attack astigmatids (Nermut et al. 2019). Their use in plant protection can expose bees to them (Erler et al. 2022). Plant parasitic worms can be much bigger, 2,000 μm or more in length (Stirling et al. 2002) and are thus unlikely to be consumed if accidentally found in the hive.

Carpoglyphus lactis as well as being a pest of stored products of high sugar content is strongly pollenophagous in the wild (Vijaykumar et al. 2013). Pollen has a high protein content (up to 35% (Anastasov 2022)) but in comparison to flower nectar or honey is poor in soluble carbohydrate content. The main group of carbohydrates are insoluble celluloses (up to 15.9% fibre content) and only small amounts of starch and sugars (Serra and Jorda 1977). Among angiosperm species, pollen grain diameter ranges from less than 10 μm (e.g., in forget-me-not, Myosotis) to over 100 μm (in some species like cotton or cucumber) (Hao et al. 2020). They are categorised as very small (< 10 μm), small (10−25 μm), medium (25−50 μm), large (50−100 μm), very large (100−200 μm), or giant (\textgreater200 μm) (Ferreira et al. 2020). So, considering the maximum effective gape of the three species herein they could only grasp small to medium grains like those of the common sunflower (Helianthus annuus) found in UK gardens (and thus in beehives), coriander, dill, and wild roses for instance (but not Hibiscus pollen, nor pollen from wheat (Golan and Pringle 2017)). Ragweed pollen at 17−23 μm could only be grabbed by C. lactis at best. Pollen grains of lucerne, various clovers and ornamental trees such as the Judas tree or the Black locust tree could be almost grasped by the chela of all three mites. However, for most plant species, most individual pollen grains are actually small to medium (ca. 20–40 μm) in size which then precludes the tyrophagid and glycyphagid herein from grasping them whole. Perhaps these taxa scrape off the oily'pollenkitt' with its high content of fats and fatty acids (Serra and Jorda 1977) that cover the pollen grains instead when in the hive.

Even though the elongate digit of C. lactis is suitable for pollenophagy, note that even C. lactis does not have the cheliceral tip design of an old fashioned'stab can-opener' like in some pollenophagous phytoseiids (Adar et al. 2012). In those mesostigmatids the fixed digit may hold the pollen down against the substrate and the moveable digit repeatedly slices into it by leverage. As among angiosperm species, pollen grain volume ranges over almost five orders of magnitude (Hao et al. 2020) and common pollens like from Mary thistle, caper spurge, white flax, blue flax, safflower, sesame, oil pumpkin and oil gourd are too large to be grasped, if astigmatids repeatedly bite into and demolish these larger pollen grains this needs examining as to how in a SEM follow-up study.

Note that the distance along the L2M axis encompassing the three small posterior teeth in C. lactis at around 5.5 μm is just in excess of the 3 μm size of the largest soil bacteria (which are normally around 1 μm in size (Luan et al. 2020)) and of the order of the diameter of the smaller fungal hyphae (at 1–3 μm (Phillott and Parmenter 2006), or 2–5 μm (Bakken and Olsen 1983)). Yeast cells (present in beehives and tree exudates) vary enormously in size. However, although the largest yeast can be as big as 40 μm, the size of an average yeast cell is between 3 and 12 μm depending upon species, so could be grasped (cracked and sheared) by the chela of all three of the species herein. Tyrophagus putrescentiae is known to feed upon various yeasts (and dermatophytes) (Duek et al. 2001).

Sclerotisation/strengthening

For C. lactis (Ca4) sclerotisation of the condyle and moveable digit scored 0 and 0, respectively. For G. domesticus (G5) sclerotisation of the condyle and moveable digit scored 3 and 3, respectively. For T. putrescentiae (T13) sclerotisation of the condyle and moveable digit scored 1 and 1, respectively. The depth of the moveable digit matches the inferred resistive forces applied by the mite to food at that point. Condylar and moveable digit strengthening by sclerotisation is associated with eating tougher food (as indicated by the F2 values).

Size of the mastication surface

The largest and smallest size of the mastication surface with which the moveable digit can rest upon any material and generate friction are respectively, 21.3 μm (C. lactis) and 17.2 μm (T. putrescentiae).

Maximum food fragment size grabbed

Maximum food fragment size grabbed by the chela is shown in Table 1. Comparing them to the overall gross gut bolus size in astigmatids yields useful insights. For instance, Hubert et al. (2004) illustrates a gastric bolus in A. siro of 11.4 μm diameter (thus approximately 782 μm³ in volume). For C. lactis, Hubert et al. (2014) illustrate gastric boli of 20.1–35.1 μm diameter (equivalent to 531–2,830 μm³ in volume). This overlaps with the scale of chelal gape in this species. On the face of it, only one maximum-gape grab of food material might yield the equivalent of a single gastric bolus in this so-called'picking' species. Erban and Hubert (2010) illustrates gastric boli in Dermatophagoides farinae and T. putrescentiae of 60.0–65.0 μm and 14.7 μm diameter respectively (thus approximately 113,097–143,793 μm³ and 1,665 μm³ in volume respectively). The bolus in T. putrescentiae must comprise more than one cheliceral grab as it is much wider than the length of the mastication surface (at 17 μm). Its volume would be equivalent to at best one grabbing bite suggesting this mite is more of a grazer or shredder than a collecting picker. Note that the hole excavated by one'bite' of the two chelicerae will be only somewhat larger than that for one chela due to the partial overlap of their calculated volumes (unless the mite moves its gnathosoma laterally between bites). Erban et al. (2016) illustrate T. putrescentiae with such gastric boli of 106.2–110.2 μm diameter (thus 627,995–701,398 μm³ in volume). This would also infer that many bites are needed to produce this suggesting it is a grazer. Using a variety of approximations, Brown et al. (2016) suggests that the total volume of the nematode Aplectus antarcticus is 39,800–97,700 μm³. This suggests that T. putrescentiae might be able to grab and tear into such sized worm-like prey if encountered in \textless100 chunks (if they can be partly grabbed – see above). More observations of T. putrescentiae feeding in the wild are needed.

Erban and Hubert (2011) states that food boli in Lepidoglyphus destructor are 80–100 μm in size. If this is a diameter then that suggests bolus volumes of 33,510–65,450 μm³. Kopeck'y et al. (2014) illustrates the gastric boli of L. destructor of 25.7 μm diameter (thus approximately 8,896 μm³ in volume). Hubert et al. (2019) also illustrates the gastric boli in D. pteronyssinus and D. farinae at 12.9–58.8 μm and 22.2–34.5 μm diameter respectively (thus approximately 1,121–106,675 μm³ and 5,710–21,587 μm³ in volume respectively). Follow-up work is needed to determine if glycyphagids and pyroglyphids are likely to be shredders or grazers based upon their bite/bolus volume ratio.

The body volume of an astigmatid can be conservatively approximated by a cylinder of idiosomal index in diameter and two times the idiosomal index in length i.e., body volume \(=\frac{Π}{2}*IL^3\) (Table 1). At least T. putrescentiae is known to be a burrowing geophage constructing pores and aerating the substrate (Robaux et al. 1977). Indeed, Bowman (2021c) classifies it (T13'A') along with C. lactis (Ca4) as an'Interstitial'. Potential cavity-living, substratum browsing / gleaning'generalist' species. On the other hand G. domesticus (G5) was classified an'Interstitial'. Potential cavity-living, possible crevice feeding / excavating'specialist'. If these three species solely used their chelicerae to dig into food material with each chelicera grabbing and tearing off a chunk every second (that was then moved away backwards out of the way immediately by their pedipalps / legs) then a hole equivalent to their estimated body volume could be excavated by a single mite in around an hour or so (Table 1). This is reasonable to believe might happen and could be critically examined by timed observations of individual mites in a follow-up experiment. Noticeably small mites (i.e., subject to higher environmental temperatures (Bowman 2021b)) in theory could excavate a body-size equivalent hole even more quickly as volume is a cube relationship to length. This time could be shorter if the mite's legs are used as digging tools too.

Morsel size pre-ingestion

The thickness values (thick) are so small that the opportunity for wide transversal ridges on digit teeth that could act as'crush-blades' of hard fibrous material like the molars of vertebrate ungulates (Schulz et al. 2010) is limited except at the nano-scale. This could be looked for in a follow-up SEM study. Note that the thickness at the condyle closely approximates the size of the input lever moment arm (L1U, Table 1) suggesting perhaps a growth process that is similar dorsoventrally as well as laterally during chelal evolution.

Morsel size pre-ingestion \(TMv_G\) figures per specimen are shown in Table 1. These morsel volumes could be compared to the typical fragment sizes found within the gastric boli of astigmatids as a validation in follow-up work. The lower limit of the measured gastric bolus volumes listed above at 1,121 μm³ (assuming that they are spherical) exceeds the size of: human sperm cells (30 μm³), red blood cells (100 μm³), lymphocytes (130 μm³), neutrophils (300 μm³) and beta cells (1,000 μm³). The range of measured gastric bolus volumes (up to 701,398 μm³) encompasses all other human individual cell volumes including fat cells at 600,000 μm³. Only, human oocytes at 4,000,000 μm³ are bigger. The bolus volumes are generally much larger than the truncated food fragment volumes calculated herein, thus needing multiple chelal grabs to form (given the wastage of material from trimming). However, some other sort of oral trituration process of grabbed food material must also be happening after the chelae engage and crush the food as many mite anatomists illustrate a tiny trans-neural mass oesophagus in acarines (of the order of 10–15 μm diameter, e.g., Alberti et al. (2003), Erban and Hubert (2011)) through which food must pass. This lumen width is only a little less than the average mastication surface length for the three species (see Table 1) so, perhaps, one chelal'grab-length' of material might be directly ingested once the distal parts of torn-off morsel were further trimmed laterally and dorsoventrally. Hubert et al. (2014) do illustrate tiny food fragments much smaller than the bolus in the caecal lumen (approximately 0.5–2 μm in diameter i.e., around \textless5 μm³ in volume), so some sort of'post-grab' processing must occur. These very tiny elements are at the scale of bacterial cells when accompanied by slime capsules (Bakken and Olsen 1983). The'end-on' SEM of the gnathosoma of the water-filled tree-hole living Naiadacarus arboricola (i.e., Figure 4B in Fashing (1998)) suggests that distally the digits themselves on their own are only about half the width of their size at the condyle. Considering this as the effective'trim width' would only reduce the estimates of the truncated food fragment size in by half (and thus divide the \(TM_G\) volume by eight in Table 1) if it was used above (rather than taking the digit width at the condyle). This is still insufficient to reduce the food sizes down enough for the smallest fragment sizes to be consilient with Hubert et al. (2014)'s photographs. i.e., even if the minimum gap between the rutella as the tips of the chelicerae digits passes between them is the important operating parameter. Further thought on a pre-ingestion trituration process of grabbed and trimmed food material (perhaps by a labrum) together with some gastric bolus forming assembly mechanism is needed. Griffiths (pers. comm.) maintained that material could be seen not just to be squeezed within the gut of astigmatids but also whirled around.

Discussion

The results are consilient with C. lactis being regarded as a fragmentary feeding'picker/collector' species. That is, this UK beehive species could pick over surfaces with its long digits (of low VR_tip and large x_ie), then slice (due to its large m and low chelal F2 force (Bowman 2021c)) the generally soft food that it collects, selectively squashing small harder elements into the smallest pre-ingestion morsels with its back teeth. The moveable digit of C. lactis is also designed to enable some degree of pollenophagy with its large maximum effective gape and large bite volume.

The results are consilient with G. domesticus being regarded as a pan-saprophagous'shredder'. That is, a possible crevice feeding/excavating specialist species, crunching (using its large chelal F2 force (Bowman 2021c)) both large and hard foodstuffs, resulting in the largest pre-ingestion morsel sizes of the three UK beehive species.

The results are consilient with T. putrescentiaee being regarded as a burrowing'browser/gleaner' generalist. That is, a fragmentary feeder with the smallest bite size of the three species, grabbing relatively small and relatively soft food morsels that are selectively squashed using its moderate chelal F2 force (Bowman 2021c).

So, although all three species should be able to grasp yeasts, spores and mycelial hyphae in the hive (Figure 3), trophic competition could be avoided.

Acknowledgements

The experimental setup and microscopical work carried out by the author in this study was: part funded under Science Research Council grant B/77307818 at Liverpool John Moores University, UK (during 1977–1979), and partly through the now defunct Pest Infestation Control Laboratory, Slough (during 1979–1983). The author declares that they have no known conflicts of interest. No competing claims are known. This article does not contain any studies with human participants or vertebrate animals. No collection permit was necessary. All data collected, generated and analysed during this study at the Oxford Centre for Industrial and Applied Mathematics and all new data generated or analysed since, plus any model specifications are included in this published article. Analysis and reporting of this study was self-funded. Thanks go to the generosity of: Valery A. Korneyev and Olga Zhovnerchuk of I. I. Schmalhausen Institute of Zoology NAS of Kyiv, Ukraine, and Serhii Filatov of National Scientific Center, ''Institute of Experimental and Clinical Veterinary Medicine'', Karkhiv, Ukraine for their great help with papers, references and illustrations by the late Prof. Igor Akimov; my friend Fred Bookstein for his long-term guidance; the late Donald E Johnston, Acarology Laboratory, Ohio State University for introducing me to the work of D'Arcy Thompson; and, Pavel Klimov and Barry OConnor, University of Michigan for repeated help with astigmatid biology and classification. Above all, I thank my wife Diane for supporting my involvement in this field over many years. The author is a Royal Society Industrial Fellow (IF110047) at the Mathematical Institute, University of Oxford.

References

1. Adar A., Inbar M., Gal S., Doron N., Zhang X-Q., Palevsky E. 2012. Plant-feeding and non-plant feeding phytoseiids: differences in behavior and cheliceral morphology. Experimental and Applied Acarology, 58(4):341-357. https://doi.org/10.1007/s10493-012-9589-y
2. Ahamad M., Louis S.R., Hamid Z., Ho T.M. 2011. Scanning electron micrographs of medically important dust mite, Suidasia pontifica (Acari: Astigmata: Saproglyphidae) in Malaysia. Tropical Biomedicine, 28(2):275-282
3. Akimov I.A. 1985. Biological foundations of harmfulness in acaroid mites. Naukova Dumka, Kiev. pp. 160 (in Russian)
4. Akimov I.A., Gaichenko V.A. 1976. The principle of action of the claws of the chelicerae in mites of the families Acaridae Leach, 1816 and Glyciphagidae Berlese, 1923 in connection with their adaptation to different food substrates. Dopovididi Akademiyi Nauk Ukrayins'koy RSR, seriya B. Heolohichni, khimichni ta biolohichni nauky, 0(4):352-355 (in Russian)
5. Alberti G., Seniczak A., Seniczak S. 2003. The digestive system and fat body of an early-derivative oribatid mite, Archegozetes longisetosus Aoki (Acari: Oribatida, Trhypochthoniidae). Acarologia, 43(1-2): 149-219.
6. Anastasov A. 2022. The Nutritional Value of Pollen. BBKA News January 2022: 10-12.
7. Bakken L.R., Olsen R.A. 1983. Buoyant Densities and Dry-Matter Contents of Microorganisms: Conversion of a Measured Biovolume into Biomass. Applied and Environmental Microbiology, 45(4):1188-1195 https://doi.org/10.1128/aem.45.4.1188-1195.1983
8. Bowman C.E. 2021a. Feeding design in free-living mesostigmatid chelicerae (Acari : Anactinotrichida). Experimental and Applied Acarology, 84(1):1-119. https://doi.org/10.1007/s10493-021-00612-8
9. Bowman C.E. 2021b. Could the acarid mite Tyrophagus putrescentiae (Schrank) be used as an environmental thermometer? International Journal of Acarology, 47(2):107-118. https://doi.org/10.1080/01647954.2021.1877350
10. Bowman C.E. 2021c. Cheliceral chelal design in Astigmatid mites. Experimental and Applied Acarology, 84(2):271-363. https://doi.org/10.1007/s10493-021-00625-3
11. Brown S., Pedley K.C., Simcock D.C. 2016. Estimation of Surface Area and Volume of a Nematode from Morphometric Data. Scientifica 2016, Article ID 6767538, 7 pp. https://doi.org/10.1155/2016/6767538
12. DeMar R., Barghusen H.R. 1973. Mechanics and the evolution of the synapsid jaw. Evolution, 26(4):622-637 https://doi.org/10.1111/j.1558-5646.1972.tb01969.x
13. Dodd J.C., Boddington C.L., Rodriguez A., Gonzalez-Chavez C., Mansur I. 2000. Mycelium of Arbuscular Mycorrhizal fungi (AMF) from different genera: form, function and detection. Plant and Soil, 226:131-151
14. Duek L., Kaufman G., Palevsky E., Berdicevsky I. 2001. Mites in fungal cultures. Mycoses, 44:390-394 https://doi.org/10.1046/j.1439-0507.2001.00684.x
15. Erban T., Hubert, J. 2010. Determination of pH in Regions of the Midguts of Acaridid Mites. Journal of Insect Science, 10(42):1-12. https://doi.org/10.1673/031.010.4201
16. Erban T., Hubert J. 2011. Visualization of protein digestion in the midgut of the acarid Lepidoglyphus destructor. Archives of Insect Biochemistry and Physiology, 78(2):74-86 https://doi.org/10.1002/arch.20441
17. Erban T., Klimov P.B., Smrz J., Phillips T.W., Nesvorna M., Kopecky J., Hubert J. 2016. Populations of Stored Product Mite Tyrophagus putrescentiae Differ in Their Bacterial Communities. Frontiers in Microbiology, 7, Article 1046, pp. 19. https://doi.org/10.3389/fmicb.2016.01046
18. Erler S., Eckert J.H., Steinert M., Alkassab A.T. 2022. Impact of microorganisms and entomopathogenic nematodes used for plant protection on solitary and social bee pollinators: Host range, specificity, pathogenicity, toxicity, and effects of experimental parameters. Environmental Pollution, 302:119051. https://doi.org/10.1016/j.envpol.2022.119051
19. Fan Q-H., Zhang Z-Q. 2007. Tyrophagus (Acari: Astigmata: Acaridae). Manaaki Whenua Press, Lincoln, New Zealand. pp. 291
20. Fashing N.J. 1998. Functional morphology as an aid in determining trophic behaviour: The placement of astigmatic mites in food webs of water-filled tree-hole communities. Experimental and Applied Acarology, 22:435-453 https://doi.org/10.1023/A:1006081622519
21. Ferreira C.T., Krug C., de Moraes G.J. 2020. Effect of pollen of different plant species on the oviposition of two phytoseiid mites (Acari: Phytoseiidae) commonly found in citrus orchards in the Brazilian Amazonia. Acarologia, 60(1):22-29. https://doi.org/10.24349/acarologia/20204360
22. Gebeshuber I.C., Gordon R. 2011. Bioinspiration for Tribological Systems on the Micro- and Nanoscale: Dynamic, Mechanic, Surface and Structure Related Functions. Micro and Nanosystems, 3:271-276 https://doi.org/10.2174/1876402911103040271
23. Gehring C.A., Wolf J.E., Theimer T.C. 2002. Terrestrial vertebrates promote arbuscular mycorrhizal fungal diversity and inoculum potential in a rain forest soil. Ecology Letters, 5:540-548 https://doi.org/10.1046/j.1461-0248.2002.00353.x
24. Golan J.J., Pringle A. 2017. Long-Distance Dispersal of Fungi. Microbiol Spectrum 5(4):FUNK-0047-2016, pp. 24. https://doi.org/10.1128/microbiolspec.FUNK-0047-2016
25. Griffiths D.A., Atyeo W.T., Norton R.A., Lynch C.A. 1990. The idiosomal chaetotaxy of astigmatid mites. Journal of Zoology, 220(1):1-32 https://doi.org/10.1111/j.1469-7998.1990.tb04291.x
26. Hammen L van der 1989. An introduction to comparative Arachnology. SPB Academic Publishing, The Hague. pp. 576
27. Hao K., Tian Z-X., Wang Z-C., Huang S-Q. 2020. Pollen grain size associated with pollinator feeding strategy. Proceedings of the Royal Society B, 287:20201191. https://doi.org/10.1098/rspb.2020.1191
28. Hubert J., Kudl'ikov'a I., Stejskal V. 2004. Review of digestive enzymes of stored product and house dust mites. Phytophaga, 14:695-710
29. Hubert J., Nesvorn'a M., Kopeck'y J., Erban T., Klimov P. 2019. Population and Culture Age Influence the Microbiome Profiles of House Dust Mites. Microbial Ecology, 77:1048-1066. https://doi.org/10.1007/s00248-018-1294-x
30. Hubert J., Nesvorn'a M., Kopeck'y J., Sagov'a-Marec^vkov'a M., Poltronieri P. 2014. Carpoglyphus lactis (Acari: Astigmata) from various dried fruits differed in associated micro-organisms. Journal of Applied Microbiology, 118:470-484 https://doi.org/10.1111/jam.12714
31. Iraola V., Prados M., Pinto H., Morales M., Leonor J.A., Carn'es J. 2015. Allergological characterisation of the storage mite Acarus gracilis (Acari: Acaridae). Allergologia et immunopathologia (Madrid), 43(4):332-338 https://doi.org/10.1016/j.aller.2014.04.004
32. Klimov P.B., OConnor B.M. 2009. Conservation of the name Tyrophagus putrescentiae, a medically and economically important mite species (Acari: Acaridae). International Journal of Acarology, 35:95-14 https://doi.org/10.1080/01647950902902587
33. Klimov P.B., OConnor B.M. 2010. Case 3501. Acarus putrescentiae Schrank, 1781 (currently Tyrophagus putrescentiae; Acariformes, ACARIDAE): proposed conservation of usage by designation of a replacement neotype. Bulletin of Zoological Nomenclature, 67(1):24-27 https://doi.org/10.21805/bzn.v67i1.a2
34. Klimov P.B., OConnor B.M. 2015. Comment on Acarus putrescentiae Schrank, 1781 (currently Tyrophagus putrescentiae; Acariformes, ACARIDAE): proposed conservation of usage by designation of a replacement neotype. Bulletin of Zoological Nomenclature, 72(1):50-56
35. Kopeck'y J., Nesvorn'a M., Hubert J. 2014. Bartonella-like bacteria carried by domestic mite species. Experimental and Applied Acarology, 64:21-32. https://doi.org/10.1007/s10493-014-9811-1
36. Luan L., Jiang Y., Cheng M., Dini-Andreote F., Sui Y., Xu Q., Geisen S., Sun B. 2020. Organism body size structures the soil microbial and nematode community assembly at a continental and global scale. Nature Communications, 11:6406. https://doi.org/10.1038/s41467-020-20271-4
37. Lynch C.A. 1989. Two new species of the genus Tyrophagus (Acari: Acaridae). Journal of Zoology, London, 219:545-567 https://doi.org/10.1111/j.1469-7998.1989.tb02600.x
38. Mariana A., Santana Raj A.S., Tan S.N., Ho T.M. 2007. Scanning electron micrographs of Blomia tropicalis (Acari: Astigmata: Echimyopodidae), a common house dust mite in Malaysia. Tropical Biomedicine, 24(2):9-37
39. Murillo P., Aguilar H., Sanchez E. 2014. Use of different SEM techniques in the study of Tyrophagus putrescentiae (Acari: Acaridae) in Costa Rica. UNED Research Journal / Cuader'nos de Investigaci'on UNED, 5(2):201-208 https://doi.org/10.22458/urj.v5i2.273
40. Nermut J., Zemek R., Mráček Z., Palevsky E, Půža V. 2019. Entomopathogenic nematodes as natural enemies for control of Rhizoglyphus robini (Acari: Acaridae)? Biological Control, 128:102-110. https://doi.org/10.1016/j.biocontrol.2018.10.003
41. Phillott A.D., Parmenter C.J. 2006. The ultrastructure of sea turtle eggshell does not contribute to interspecies variation in fungal invasion of the egg. Canadian Journal of Zoology, 84:1339-1344. https://doi.org/10.1139/z06-125
42. Robaux P., Jeanson C.Y., Barbier D. 1977. Microstructures construites par un acarien Tyrophagus putrescentiae dans une argile. Etude experimentale et microscopique. Ecological Bulletins 25, Soil Organisms as Components of Ecosystems, pp. 489-493, Oikos Editorial Office. https://www.jstor.org/stable/20112618
43. Schulz E., Calandra I., Kaiser T.M. 2010. Applying tribology to teeth of hoofed mammals. Scanning, 32(4)162-182. https://doi.org/10.1002/sca.20181
44. Serra Bobvehi J., Jorda R.E. 1977. Nutrient composition and microbiological quality of honey-bee collected pollen in Spain. Journal of Agriculture and Food Chemistry, 45:725-732 https://doi.org/10.1021/jf960265q
45. Stirling G., Nicol J., Reay F. 2002. Advisory Services for Nematode Pests. Operational Guidelines. Rural Industries Research and Development Corporation, Australia. Publication No. 99/41. Project No. AAN-2A. pp. 119
46. Su X., Fang Y., Xu J-Y., Fang W-X., Zhan X-B., Fang Y., Chu L-M., Feng R., Jin Y-L., Sun E-T. 2020. The complete mitochondrial genome of the storage mite pest Tyrophagus fanetzhangorum (Acari: Acaridae). Systematic and Applied Acarology, 25(9):1693-1701. https://doi.org/10.11158/saa.25.9.14
47. Vijayakumar K., Muthuraman M., Jayaraj R. 2013. Infestation of Carpoglyphus lactis (Linnaeus) (Acari: Carpoglyphidae) on Trigona iridipennis (Apidae: Meliponinae) from India. Scholarly Journal of Agricultural Science, 3(1):25-28
48. Wirth S. 2006. Morphology and function of the gnathosoma in the Histiostomatidae (Astigmata). Acarologia, 46(1-2):103-109

instructions